 时,桌面上有一质量为M,初始高度为
时,桌面上有一质量为M,初始高度为 ,半径恒定为
,半径恒定为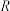 ,电荷量密度
,电荷量密度 ,质量和密度均匀分布,杨氏模量为A的绝缘弹性体,圆柱体底面时刻与地面相连,可绕中心无摩擦转动;全空间电磁场只考虑在
,质量和密度均匀分布,杨氏模量为A的绝缘弹性体,圆柱体底面时刻与地面相连,可绕中心无摩擦转动;全空间电磁场只考虑在 方向上的
方向上的 ,
,  ,(
,( ), 以及该磁场附加的涡旋电场;随着时间变化,圆柱体在
), 以及该磁场附加的涡旋电场;随着时间变化,圆柱体在 方向电场力作用下,上下周期性运动,质量、电荷密度变得不均匀,并且由于电场较大可认为各处在
方向电场力作用下,上下周期性运动,质量、电荷密度变得不均匀,并且由于电场较大可认为各处在 方向上时时受力平衡,即拉力与电场力平衡,同时在涡旋电场力矩下开始转动,本题探究仅在该两项电场力作用足够长时间后:
方向上时时受力平衡,即拉力与电场力平衡,同时在涡旋电场力矩下开始转动,本题探究仅在该两项电场力作用足够长时间后: ;
; 轴转角可近似为
轴转角可近似为 的形式,求
的形式,求
 的初速度竖直上抛一小球;经过
的初速度竖直上抛一小球;经过 时间后在楼顶边缘从静止开始释放另一小球.若要求两小球同时落地,忽略空气阻力,则
时间后在楼顶边缘从静止开始释放另一小球.若要求两小球同时落地,忽略空气阻力,则 的取值范围和抛出点的高度应为 [ ]
的取值范围和抛出点的高度应为 [ ]A. , , |
B. , , |
C. , , |
D. , , |
 截面积为A的磁介质上绕有
截面积为A的磁介质上绕有 匝线圈,接上电源。改变电流的大小以改变介质中的磁场
匝线圈,接上电源。改变电流的大小以改变介质中的磁场 ,试计算电源克服线圈中感生电动势所做的功
,试计算电源克服线圈中感生电动势所做的功 。假设磁介质在磁化过程中体积和压强不变;
。假设磁介质在磁化过程中体积和压强不变; ,其中
,其中 、
、 分别表示磁化强度和磁场强度保持不变时,磁介质的热容,角标S表示等熵过程(即绝热);
分别表示磁化强度和磁场强度保持不变时,磁介质的热容,角标S表示等熵过程(即绝热); ,其中
,其中 称为居里系数,且
称为居里系数,且 。试求
。试求 (用两个热力学参量表示,如
(用两个热力学参量表示,如 和
和 );
); 、
、 以及一个积分常数;
以及一个积分常数; 展开为
展开为 ,由于
,由于 相对于
相对于 是对称的,因此展开式中只有
是对称的,因此展开式中只有 的偶数次项。进一步假设临界点附近满足
的偶数次项。进一步假设临界点附近满足 ,
,  , 且
, 且 ,
, ,求系统在
,求系统在 和
和 时平衡态的磁化强度
时平衡态的磁化强度 、自由能
、自由能 及零场比热
及零场比热 ,并判断相变的级数
,并判断相变的级数 ,试计算临界点附近系统的磁化强度
,试计算临界点附近系统的磁化强度 以及零场磁化率
以及零场磁化率 ;
; ,我们需要将
,我们需要将 进一步展开以保证系统的稳定性
进一步展开以保证系统的稳定性 , 假设a、b的形式不变,
, 假设a、b的形式不变, ,且
,且 ,
, ,
, ,试求出系统的平衡态磁化强度
,试求出系统的平衡态磁化强度 ,发生相变的温度
,发生相变的温度 (用
(用 表示),并判断相变的级数;
表示),并判断相变的级数; 的对称性被破缺,需要在自由能中引入奇数阶项,如
的对称性被破缺,需要在自由能中引入奇数阶项,如 ,假设a、b的形式不变,
,假设a、b的形式不变, ,且
,且 ,
, ,
, ,试求出系统的平衡态磁化强度
,试求出系统的平衡态磁化强度 ,发生相变的温度
,发生相变的温度 (用
(用 表示),并判断相变的级数。
表示),并判断相变的级数。 
A.当Um< 时,所有电子都能从极板的右端射出 时,所有电子都能从极板的右端射出 |
B.当Um> 时,将没有电子能从极板的右端射出 时,将没有电子能从极板的右端射出 |
C.当 时,有电子从极板右端射出的时间与无电子从极板右端射出的时间之比为1:2 时,有电子从极板右端射出的时间与无电子从极板右端射出的时间之比为1:2 |
D.当 时,有电子从极板右端射出的时间与无电子从极板右端射出的时间之比为1: 时,有电子从极板右端射出的时间与无电子从极板右端射出的时间之比为1: |
 时刻由静止释放两球,两球在竖直面内做无序运动;
时刻由静止释放两球,两球在竖直面内做无序运动; 时刻,细杆a与竖直方向的夹角
时刻,细杆a与竖直方向的夹角 ,小球N恰好到达与O点等高处且速度方向水平向右。重力加速度为g,不计摩擦和空气阻力
,小球N恰好到达与O点等高处且速度方向水平向右。重力加速度为g,不计摩擦和空气阻力
 时刻,小球M的速度方向
时刻,小球M的速度方向 过程中,a、b两杆对M球做功之和为
过程中,a、b两杆对M球做功之和为 过程中,细杆b对N球的冲量大小为
过程中,细杆b对N球的冲量大小为 、沿着y、z方向无限延展的金属平板,位于
、沿着y、z方向无限延展的金属平板,位于 区域;而
区域;而 区域为真空,电场为零。将金属内的导电电子视为在空间均匀的正电荷背景上运动的经典理想气体。没有温度梯度时,呈电中性的金属内部的电子是完全均匀分布的,其数密度为
区域为真空,电场为零。将金属内的导电电子视为在空间均匀的正电荷背景上运动的经典理想气体。没有温度梯度时,呈电中性的金属内部的电子是完全均匀分布的,其数密度为 ;有温度梯度时,金属内的温度是x的函数,
;有温度梯度时,金属内的温度是x的函数, ,且
,且 。在(局域)热平衡状态下,金属内电子数密度
。在(局域)热平衡状态下,金属内电子数密度 会略微偏离
会略微偏离 ,
, 。金属内部也会有很小的沿x方向的电场
。金属内部也会有很小的沿x方向的电场 。金属表面
。金属表面 内侧也分别有很小的面电荷密度
内侧也分别有很小的面电荷密度 和
和 。已知电子质量为m,所带电荷为
。已知电子质量为m,所带电荷为 。忽略重力,玻尔兹曼常量为
。忽略重力,玻尔兹曼常量为 。
。 的不均匀性会引起粒子的扩散。若在时间间隔
的不均匀性会引起粒子的扩散。若在时间间隔 内通过
内通过 平面上面积为
平面上面积为 的粒子数为
的粒子数为 ,则
,则 被称为粒子流密度。粒子扩散流密度
被称为粒子流密度。粒子扩散流密度 满足斐克(Fick)定律
满足斐克(Fick)定律 ,式中D是扩散系数
,式中D是扩散系数 这里,c是已知常量。在平衡状态下,金属内部应该没有净的电流,因此前述的电子扩散流会被内部电场产生的漂移电流抵消。为简化起见,设金属的电阻率
这里,c是已知常量。在平衡状态下,金属内部应该没有净的电流,因此前述的电子扩散流会被内部电场产生的漂移电流抵消。为简化起见,设金属的电阻率 是与
是与 等无关的已知常量。求金属板内部电场
等无关的已知常量。求金属板内部电场 的表达式(用
的表达式(用 、
、 、
、 和其他常量表出)。
和其他常量表出)。 满足的微分方程:并利用(1)的结果消去电场
满足的微分方程:并利用(1)的结果消去电场 ,导出
,导出 满足的微分方程和边界条件。真空介电常量为
满足的微分方程和边界条件。真空介电常量为 。(提示:净的电荷密度包含正电荷背景)
。(提示:净的电荷密度包含正电荷背景) 、
、 等小量的线性项,解出
等小量的线性项,解出 (解中可包含
(解中可包含 和
和 )。
)。 不为零,但在任意x处电子气(可视为理想气体)处于局域热平衡;电子气中的电子受到电场
不为零,但在任意x处电子气(可视为理想气体)处于局域热平衡;电子气中的电子受到电场 的作用,但厚度为
的作用,但厚度为 的薄层内的电子气仍处于宏观的力学平衡状态。试导出
的薄层内的电子气仍处于宏观的力学平衡状态。试导出 满足的微分方程,并将其线性化。再利用(3)的结果,求出
满足的微分方程,并将其线性化。再利用(3)的结果,求出 。
。 和
和 )的电势差和温度差的比值(即金属的Seebeck系数S)
)的电势差和温度差的比值(即金属的Seebeck系数S) 。附注:对金属温差电现象的正确分析必须考虑电子的量子效应,本题目中的简化经典模型并不适用于真实情况。
。附注:对金属温差电现象的正确分析必须考虑电子的量子效应,本题目中的简化经典模型并不适用于真实情况。
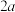 、质量为m的匀质刚性细杆,其一端有一小孔,嵌套在半径为R的水平圆环的P点处(P是圆环上的固定点);P点(连同杆)随圆环一起绕圆环中心轴以恒定角速度
、质量为m的匀质刚性细杆,其一端有一小孔,嵌套在半径为R的水平圆环的P点处(P是圆环上的固定点);P点(连同杆)随圆环一起绕圆环中心轴以恒定角速度 转动;同时,杆可绕P点无摩擦地转动,且杆和圆环矢径
转动;同时,杆可绕P点无摩擦地转动,且杆和圆环矢径 始终在同一竖直平面内;杆与竖直方向之间夹角为
始终在同一竖直平面内;杆与竖直方向之间夹角为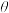 。重力加速度大小为g。
。重力加速度大小为g。 转动的转动参考系S中,写出杆的机械能表达式(表达式中可以含有
转动的转动参考系S中,写出杆的机械能表达式(表达式中可以含有 );
);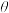 所需满足的条件;
所需满足的条件; )、Ⅱ(
)、Ⅱ( )、Ⅲ(
)、Ⅲ( )和Ⅳ(
)和Ⅳ( )象限中,分别可能出现的杆的平衡位形的数目,以及相应的a、R、
)象限中,分别可能出现的杆的平衡位形的数目,以及相应的a、R、 各参量之间需要满足的条件;
各参量之间需要满足的条件;
 轴角动量,然后硬币掉落在摩擦系数极小的光滑桌面上,因此能量损失会较为缓慢,能作为准静态考虑。硬币边缘对于桌面是纯滚的,旋转过程可以看作是旋转对称的。设硬币(抽象成一个均质圆柱体)厚度为
轴角动量,然后硬币掉落在摩擦系数极小的光滑桌面上,因此能量损失会较为缓慢,能作为准静态考虑。硬币边缘对于桌面是纯滚的,旋转过程可以看作是旋转对称的。设硬币(抽象成一个均质圆柱体)厚度为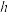 ,半径为
,半径为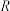 ,质量为
,质量为 ,请回答下列问题:
,请回答下列问题: 轴为硬币的主轴(原点在质心),求转动惯量
轴为硬币的主轴(原点在质心),求转动惯量 ;
;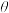 时的旋转。假定
时的旋转。假定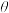 在一个周期内不会改变,改变的只是硬币平面的方向,硬币的质心在周期内可认为不动的。我们定义经过质心、垂直于硬币平面向上为
在一个周期内不会改变,改变的只是硬币平面的方向,硬币的质心在周期内可认为不动的。我们定义经过质心、垂直于硬币平面向上为 轴,由硬币质心指向接触点所在母线中点为
轴,由硬币质心指向接触点所在母线中点为 轴,
轴, 轴参照右手系原则定义。同样的,你也可以定义实际的
轴参照右手系原则定义。同样的,你也可以定义实际的 轴,
轴, 轴垂直于桌面向上,
轴垂直于桌面向上, 轴正方向定义为硬币质心对于桌面的投影指向硬币与桌面接触点,
轴正方向定义为硬币质心对于桌面的投影指向硬币与桌面接触点, 轴与
轴与 轴指向相同。请求出(可认为
轴指向相同。请求出(可认为 ,认为无摩擦力,以后
,认为无摩擦力,以后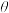 均按照此定义)
均按照此定义) 轴正方向)
轴正方向) ;
; (即从硬币在顶上看花纹的运动角速度,可以用转一圈花纹的角位移除以转一圈用时来计算);
(即从硬币在顶上看花纹的运动角速度,可以用转一圈花纹的角位移除以转一圈用时来计算);
 是硬币与桌面接触点在桌面上的运动速度(注意:接触点是硬币与桌面的接触点,不是硬币上固定的一点)。请求出在
是硬币与桌面接触点在桌面上的运动速度(注意:接触点是硬币与桌面的接触点,不是硬币上固定的一点)。请求出在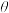 较小时角度
较小时角度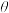 与时间
与时间 的关系(假定
的关系(假定 时
时 ),并给出发出响声的频率
),并给出发出响声的频率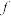 与时间
与时间 的关系。你可以假定初态
的关系。你可以假定初态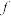 为
为 。
。

A.超声波的速度为 |
B.超声波的速度为 |
C.物体的平均速度为 |
D.物体的平均速度为 |
 的直轨道,小滑块从轨道上A点静止释放,其下方右侧放置一水平传送带,传送带与直轨道末端B间距很小,但允许小滑块从左端滑出。传送带以恒定速度
的直轨道,小滑块从轨道上A点静止释放,其下方右侧放置一水平传送带,传送带与直轨道末端B间距很小,但允许小滑块从左端滑出。传送带以恒定速度 逆时针转动,水平部分CD长度L = 2m。设释放点A与B距离为s,小滑块从直轨道B端运动到达传送带上C点时,速度大小不变,方向变为水平向右。已知小滑块与直轨道间的动摩擦因数
逆时针转动,水平部分CD长度L = 2m。设释放点A与B距离为s,小滑块从直轨道B端运动到达传送带上C点时,速度大小不变,方向变为水平向右。已知小滑块与直轨道间的动摩擦因数 ,与传送带间的动摩擦因数
,与传送带间的动摩擦因数 ,且滑块相对传送带滑动时能在传送带上留下清晰划痕,传送带足够长。(
,且滑块相对传送带滑动时能在传送带上留下清晰划痕,传送带足够长。( ,
, )
) ,求小滑块从A运动到B所需的时间;
,求小滑块从A运动到B所需的时间; ,求小滑块在传送带上留下的划痕长度;
,求小滑块在传送带上留下的划痕长度; 的值,设小滑块从传送带上滑离后在传送带上留下的划痕长度为
的值,设小滑块从传送带上滑离后在传送带上留下的划痕长度为 ,求
,求 与
与 的关系式。
的关系式。