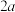搜索
、质量为m的匀质刚性细杆，其一端有一小孔，嵌套在半径为R的水平圆环的P点处（P是圆环上的固定点）；P点（连同杆）随圆环一起绕圆环中心轴以恒定角速度
转动；同时，杆可绕P点无摩擦地转动，且杆和圆环矢径
始终在同一竖直平面内；杆与竖直方向之间夹角为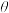
。重力加速度大小为g。（1）将所有类型的保守力做功都与势能变化相联系，试分别在实验室系L和在随矢径
转动的转动参考系S中，写出杆的机械能表达式（表达式中可以含有
）；（2）在S参考系中导出杆处于平衡位形时，
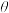所需满足的条件；（3）在S参考系中，对于第（2）问中得到的结果，利用图解法分析0取值在Ⅰ（
）、Ⅱ（
）、Ⅲ（
）和Ⅳ（
）象限中，分别可能出现的杆的平衡位形的数目，以及相应的a、R、各参量之间需要满足的条件；（4）在S参考系中，分象限画出对杆所受到的相对于P点的力矩有贡献的受力示意图（对于分布性的力，仅需示意性地画出其对P点力矩有贡献的等效合力），查看是否可能出现平衡位形，以检验（3）中分析的结果；
（5）试讨论（3）中所确定的杆的各个平衡位形的稳定性。
同类型试题
y = sin x， x∈R， y∈[–1，1]，周期为2π，函数图像以 x = (π/2) + kπ 为对称轴
y = arcsin x， x∈[–1，1]， y∈[–π/2，π/2]
sin x = 0 ←→ arcsin x = 0
sin x = 1/2 ←→ arcsin x = π/6
sin x = √2/2 ←→ arcsin x = π/4
sin x = 1 ←→ arcsin x = π/2
y = sin x， x∈R， y∈[–1，1]，周期为2π，函数图像以 x = (π/2) + kπ 为对称轴
y = arcsin x， x∈[–1，1]， y∈[–π/2，π/2]
sin x = 0 ←→ arcsin x = 0
sin x = 1/2 ←→ arcsin x = π/6
sin x = √2/2 ←→ arcsin x = π/4
sin x = 1 ←→ arcsin x = π/2
