 处有一质量为
处有一质量为 ,带电量为q的质点,空间中存在均匀的磁场B,且存在以O为圆心电荷密度为
,带电量为q的质点,空间中存在均匀的磁场B,且存在以O为圆心电荷密度为 半径为
半径为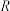 的球形区域。
的球形区域。 为运动中的守恒量,并求出
为运动中的守恒量,并求出 的值。
的值。 处释放,释放时质点速度为0,若
处释放,释放时质点速度为0,若 ,试求质点所能达到的最远距离及最近距离
,试求质点所能达到的最远距离及最近距离 ,
, ,在本题中,认为质点始终不超过半径为
,在本题中,认为质点始终不超过半径为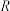 的球形区域。
的球形区域。 处释放,释放时质点速度为0,若
处释放,释放时质点速度为0,若 ,且
,且 ,试求极坐标下粒子的位置随时间的关系, 认为质点始终没有进入半径为R的球形区域。
,试求极坐标下粒子的位置随时间的关系, 认为质点始终没有进入半径为R的球形区域。 
| A.电阻中的电流方向由a到b |
B.电阻R的电功率为 |
C.电源的总功率为 |
| D.增大两金属板的正对面积可增大发电机的电动势 |
 的物体上有一个向下凹陷的旋转椭球面。其竖直方向截面的椭圆的半长轴为b,半短轴为a。在其边缘从静止释放一个质量为m的小球。忽略所有可能的摩擦。
的物体上有一个向下凹陷的旋转椭球面。其竖直方向截面的椭圆的半长轴为b,半短轴为a。在其边缘从静止释放一个质量为m的小球。忽略所有可能的摩擦。 。
。
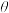 相连,一束光平行于一个反射面入射,试求光线的反射次数与
相连,一束光平行于一个反射面入射,试求光线的反射次数与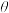 的关系,再考虑这样的一个系统,将质量分别为
的关系,再考虑这样的一个系统,将质量分别为 ,
, 的滑块按如图所示的方式摆放在光滑地面上,给予
的滑块按如图所示的方式摆放在光滑地面上,给予 一个向左的速度v,之后
一个向左的速度v,之后 ,
, 之间,
之间, 与墙之间将发生数次完全弹性碰撞,记上述碰撞次数总和为
与墙之间将发生数次完全弹性碰撞,记上述碰撞次数总和为 。
。 ,计算
,计算 。
。 坐标系,其中
坐标系,其中 ,
, ,其中
,其中 为
为 右端距墙面的距离,
右端距墙面的距离, 为
为 左端距墙面的距离,请定性在坐标系中作出描述
左端距墙面的距离,请定性在坐标系中作出描述 ,
, 运动的图像,要求作出:
运动的图像,要求作出: 坐标轴;
坐标轴; ,
, 发生碰撞条件;
发生碰撞条件; 和墙发生碰撞的条件;
和墙发生碰撞的条件; ,
, 的运动,用带箭头的线段表示运动路径,用
的运动,用带箭头的线段表示运动路径,用 表示碰撞点,用
表示碰撞点,用 表示运动先后,若轨迹有重合,请稍微错开。
表示运动先后,若轨迹有重合,请稍微错开。 ,在上述坐标系中作出表示
,在上述坐标系中作出表示 ,
, 第一次碰撞的曲线,用
第一次碰撞的曲线,用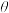 、
、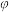 分别表示第一次碰撞发生前后曲线与
分别表示第一次碰撞发生前后曲线与 ,
, 发生碰撞条件的夹角(用参量
发生碰撞条件的夹角(用参量 ,
, ,
, 表示)
表示) ,
, ,重新在
,重新在 坐标系中作出:
坐标系中作出: ,
, 发生碰撞条件;
发生碰撞条件; 和墙发生碰撞的条件,并写出表示坐标系中对于
和墙发生碰撞的条件,并写出表示坐标系中对于 ,
, 碰撞条件最重要的参量(用参量
碰撞条件最重要的参量(用参量 ,
, ,v表示)
,v表示) ,在坐标系中作出描述
,在坐标系中作出描述 ,
, 运动及碰撞的图像,用带箭头的线段表示运动路径,用
运动及碰撞的图像,用带箭头的线段表示运动路径,用 表示碰撞点,用
表示碰撞点,用 表示运动先后,画出三次碰撞即可。
表示运动先后,画出三次碰撞即可。 的近似条件,试求
的近似条件,试求 的值;特别的,当
的值;特别的,当 时,求
时,求 值,当
值,当 时,求
时,求 值,再求
值,再求 。
。
 。折杆的两边长度都和圆筒半径相等。
。折杆的两边长度都和圆筒半径相等。 端恰好位于同一竖直线上,且系统初态静止;试求系统释放后瞬间折杆角加速度
端恰好位于同一竖直线上,且系统初态静止;试求系统释放后瞬间折杆角加速度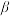 ,试求释放后当
,试求释放后当 边恰好达到竖直时折杆的角速度
边恰好达到竖直时折杆的角速度 ;
; 端恰好位于同一水平线上,且系统静止。此时对折杆施加微小扰动,试求系统振动频率
端恰好位于同一水平线上,且系统静止。此时对折杆施加微小扰动,试求系统振动频率

 在这个反应中,来自加速器的高能质子撞击静质子而产生
在这个反应中,来自加速器的高能质子撞击静质子而产生 介子和氘核D。已知质子、
介子和氘核D。已知质子、  介子和氘核D的静止质量分别为:
介子和氘核D的静止质量分别为:
 ,即,使上述反应得以进行的最小入射质子动能。
,即,使上述反应得以进行的最小入射质子动能。 两倍,试计算该反应中产生的
两倍,试计算该反应中产生的 介子的动量的可能的最大值。
介子的动量的可能的最大值。 介子的概率相同。求:在实验室参照系中,在质子入射方向上单位立体角内产生一个
介子的概率相同。求:在实验室参照系中,在质子入射方向上单位立体角内产生一个 介子的概率。
介子的概率。  求和是对整个多质点的系统进行的,其中
求和是对整个多质点的系统进行的,其中 是第
是第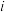 个质点的动量,
个质点的动量, 是第
是第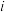 个质点的位置矢量。我们把
个质点的位置矢量。我们把 对时间求导,我们假设这个系统是处于周期性的稳态下的,求
对时间求导,我们假设这个系统是处于周期性的稳态下的,求 对时间的导数的时间平均值。
对时间的导数的时间平均值。 。那么请讨论系统总动能和总势能之间满足的数学关系。
。那么请讨论系统总动能和总势能之间满足的数学关系。 和分子平均动能
和分子平均动能 ,分子数密度
,分子数密度 的关系。我们假设理想气体分子之间没有任何的相互作用。
的关系。我们假设理想气体分子之间没有任何的相互作用。 和分子平均动能
和分子平均动能 ,分子数密度
,分子数密度 的关系
的关系 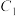 和
和 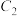 , 且它们之间的互容系数为
, 且它们之间的互容系数为  , 则
, 则  , 且
, 且  。考虑四块的面积为
。考虑四块的面积为 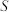 的平行极板, 依次编号为 a–d。 极板 a 和极板 c 看作一个电容器, 极板间距为
的平行极板, 依次编号为 a–d。 极板 a 和极板 c 看作一个电容器, 极板间距为  ; 极板 b 和极板 d 看作一个电容器, 极板间距为
; 极板 b 和极板 d 看作一个电容器, 极板间距为  ; 极板 b 和极板 c 的间距为
; 极板 b 和极板 c 的间距为 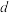 。 其中
。 其中  , 且
, 且  。
。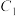 与
与 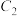 , 电感
, 电感  与
与 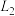 。 两个电容之间的互容系数为
。 两个电容之间的互容系数为  , 两个电感之间的互感系数为
, 两个电感之间的互感系数为  。 求电路的振动频率。 若该振动由多个频率不同的简谐振动叠加而成, 求出所有的频率。
。 求电路的振动频率。 若该振动由多个频率不同的简谐振动叠加而成, 求出所有的频率。  。 显然存在一条过 O 的轴 z 使得三锟闸绕 z 轴有
。 显然存在一条过 O 的轴 z 使得三锟闸绕 z 轴有  旋转对称。 z 轴与地面的夹角被适当地选取, 以至于三锟闸在初始状态可以与地面达成这样一种相对位形∶ 其中一根杆与地面平行, 另外两根杆的自由端的连线也与地面平行。 有一堵固定在地面上的墙, 其位置满足∶ 在初始状态下, 三锟闸的水平杆垂直于墙, 且墙面紧贴在水平杆的自由端。 将通过闸机的人简化为刚性长方体。 人通过闸机的过程中, 长方体推动三锟闸绕 z 轴转动, 长方体的一个面紧贴地面, 另一个面紧贴墙面。长方体足够高。
旋转对称。 z 轴与地面的夹角被适当地选取, 以至于三锟闸在初始状态可以与地面达成这样一种相对位形∶ 其中一根杆与地面平行, 另外两根杆的自由端的连线也与地面平行。 有一堵固定在地面上的墙, 其位置满足∶ 在初始状态下, 三锟闸的水平杆垂直于墙, 且墙面紧贴在水平杆的自由端。 将通过闸机的人简化为刚性长方体。 人通过闸机的过程中, 长方体推动三锟闸绕 z 轴转动, 长方体的一个面紧贴地面, 另一个面紧贴墙面。长方体足够高。 ∶ 人能完全通过闸机, 且长方体的厚度可以任意大。
∶ 人能完全通过闸机, 且长方体的厚度可以任意大。 , 求满足以下条件的长方体的最大横截面积∶ 人能完全通过闸机。 只需写出它是什么函数在什么区间上的最大值即可。
, 求满足以下条件的长方体的最大横截面积∶ 人能完全通过闸机。 只需写出它是什么函数在什么区间上的最大值即可。 。 人在完全通过闸机的过程中, 与杆之间存在滑动摩擦, 摩擦系数为
。 人在完全通过闸机的过程中, 与杆之间存在滑动摩擦, 摩擦系数为 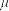 。 在三锟闸的转轴内有滑动摩擦力矩, 其大小恒定为 K。 求人在缓慢地完全通过闸机的过程中, 对杆做的功。 可以保留积分。
。 在三锟闸的转轴内有滑动摩擦力矩, 其大小恒定为 K。 求人在缓慢地完全通过闸机的过程中, 对杆做的功。 可以保留积分。
 ,圆柱轮由外半径为
,圆柱轮由外半径为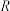 ,内半径为
,内半径为 ,质量为
,质量为 的圆柱壳和总质量为
的圆柱壳和总质量为 的8根辐条组成。质量为
的8根辐条组成。质量为 的车身对称地架在轮子上(车身与轮轴之间是固定的,其长为
的车身对称地架在轮子上(车身与轮轴之间是固定的,其长为 ,厚度为
,厚度为 。前后轮中心之间间距为
。前后轮中心之间间距为 ,圆柱轮中心到车身底部距离为
,圆柱轮中心到车身底部距离为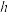 。忽略圆柱轮与轴之间的摩擦和支撑车身架子的质量。重力加速度为
。忽略圆柱轮与轴之间的摩擦和支撑车身架子的质量。重力加速度为 ,轮子与地面的静摩擦系数与动摩擦系数均为
,轮子与地面的静摩擦系数与动摩擦系数均为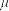 。
。 ,求
,求 的值(用分数表示);(之后涉及有关圆柱车轮转动惯量的量均用
的值(用分数表示);(之后涉及有关圆柱车轮转动惯量的量均用 表示不用带入具体数值)
表示不用带入具体数值) 。假设没有轮子脱离地面。引入无量纲常数
。假设没有轮子脱离地面。引入无量纲常数 ,若前后轮均做纯滚动,求刚刹车时加速度
,若前后轮均做纯滚动,求刚刹车时加速度 ,前后轮均做纯滚动时,
,前后轮均做纯滚动时, 满足的条件,以及没有轮子脱离地面的条件;
满足的条件,以及没有轮子脱离地面的条件; ,前轮纯滚动、后轮滑动时
,前轮纯滚动、后轮滑动时 满足的条件,能达到前轮纯滚动、后轮滑动时
满足的条件,能达到前轮纯滚动、后轮滑动时 满足的条件,以及没有轮子脱离地面的条件;
满足的条件,以及没有轮子脱离地面的条件; 。
。