学进去

某地铁站的出入站闸机采用三锟闸设计。 三锟闸是这样一种装置∶ 考虑三维空间中的三根长度均为 l 的细硬轻杆， 每根杆都有一端被固定在点 O 处， 且它们两两之间的夹角被固定为 。 显然存在一条过 O 的轴 z 使得三锟闸绕 z 轴有 旋转对称。 z 轴与地面的夹角被适当地选取， 以至于三锟闸在初始状态可以与地面达成这样一种相对位形∶ 其中一根杆与地面平行， 另外两根杆的自由端的连线也与地面平行。 有一堵固定在地面上的墙， 其位置满足∶ 在初始状态下， 三锟闸的水平杆垂直于墙， 且墙面紧贴在水平杆的自由端。 将通过闸机的人简化为刚性长方体。 人通过闸机的过程中， 长方体推动三锟闸绕 z 轴转动， 长方体的一个面紧贴地面， 另一个面紧贴墙面。长方体足够高。
（1）求满足以下条件的长方体的最大宽度 ∶ 人能完全通过闸机， 且长方体的厚度可以任意大。
（2）接上问， 若长方体的宽度大于 ， 求满足以下条件的长方体的最大横截面积∶ 人能完全通过闸机。 只需写出它是什么函数在什么区间上的最大值即可。
（3）长方体的宽度为 。 人在完全通过闸机的过程中， 与杆之间存在滑动摩擦， 摩擦系数为 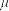。 在三锟闸的转轴内有滑动摩擦力矩， 其大小恒定为 K。 求人在缓慢地完全通过闸机的过程中， 对杆做的功。 可以保留积分。