搜索
（1）我们定义这样一个量：
求和是对整个多质点的系统进行的，其中
是第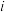
个质点的动量，
是第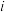个质点的位置矢量。我们把
对时间求导，我们假设这个系统是处于周期性的稳态下的，求对时间的导数的时间平均值。（2）我们假设这个系统的相互作用势能的形式如下
。那么请讨论系统总动能和总势能之间满足的数学关系。（3）接上小问，请求出在天体系统和弹簧系统中的数学关系。
（4）本小问讨论位力定理在热力学系统中的应用。
①利用上一问的结论，请推导出理想气体压强
和分子平均动能
，分子数密度
的关系。我们假设理想气体分子之间没有任何的相互作用。②接上小问，请推出光子气体系统中的压强
和分子平均动能，分子数密度的关系
同类型试题
y = sin x， x∈R， y∈[–1，1]，周期为2π，函数图像以 x = (π/2) + kπ 为对称轴
y = arcsin x， x∈[–1，1]， y∈[–π/2，π/2]
sin x = 0 ←→ arcsin x = 0
sin x = 1/2 ←→ arcsin x = π/6
sin x = √2/2 ←→ arcsin x = π/4
sin x = 1 ←→ arcsin x = π/2
y = sin x， x∈R， y∈[–1，1]，周期为2π，函数图像以 x = (π/2) + kπ 为对称轴
y = arcsin x， x∈[–1，1]， y∈[–π/2，π/2]
sin x = 0 ←→ arcsin x = 0
sin x = 1/2 ←→ arcsin x = π/6
sin x = √2/2 ←→ arcsin x = π/4
sin x = 1 ←→ arcsin x = π/2
