考虑这样一种“光栅”,它们像寻常的衍射光栅一样有密集分布的条纹,用于遮挡光线。我们所使用的光的波长的尺度远小于条纹的细节,所以实际上无法观察到衍射现象。当一束均匀的平行光垂直射入光栅时,光栅背后的光屏上会展示出条纹。它们不是光的干涉或衍射条纹,暗纹的出现仅仅是因为本应到达该处的光被光栅上的条纹遮挡。当我们远远地观看光屏时,因为眼睛的辨别能力有限(即条纹间距远小于Rayleigh判据的要求),实际上观察到的是一片亮度随空间分布的光斑,越暗的地方条纹越密。我们定义观察到的光斑在

处的亮度为,在

处取的一块小面积

(虽然很小,但其尺度远大于条纹的细节)上未被条纹遮挡的部分的面积占比。
(1)现在我们制作了两个相同的光栅,光栅上均匀分布着平直的条纹,条纹宽度都为
d,条纹之间的间隙都为
p。现在将两个光栅倾斜摆放,使得它们的条纹与
x轴的夹角分别为
θ和-
θ。两个光栅关于
y轴对称。将这两个倾斜摆放的光栅贴在一起后得到一个新的光栅。求均匀的平行光垂直通过这一光栅之后光屏上得到的亮度分布

。量级

。
(2)现在我们制作了两个相似的光栅,光栅上分布着同心圆形状的条纹。其中一个光栅的条纹的宽度和条纹之间的间隙都为

,条纹的圆心在

。另一个光栅的条纹的宽度和条纹之间的间隙都为

,条纹的圆心在

。将这两个光栅贴在一起后得到一个新的光栅。求均匀的平行光垂直通过这一光栅之后在光屏上得到的亮度分布

。量级

。
(3)接上一问,在极坐标下求暗纹中心的曲线方程;求暗纹的数量有限的条件;在暗纹的数量有限的条件下求暗纹的数量。
 B.
B.  C.
C.  D.
D.

 ,则通过计算机拟合得出y-x图线如图(2)所示,则图线最高点A点的坐标x=
,则通过计算机拟合得出y-x图线如图(2)所示,则图线最高点A点的坐标x=


 时,小球的动能等于重力势能b
时,小球的动能等于重力势能b

 、方向水平向右的匀强电场中。把一带电量
、方向水平向右的匀强电场中。把一带电量 的小滑块A从距离B左侧L=0.75m处由静止释放,A与B正碰后瞬间粘在一起。已知A、B、C三者的质量均为m=1kg,A、B与C间的动摩擦因数均为
的小滑块A从距离B左侧L=0.75m处由静止释放,A与B正碰后瞬间粘在一起。已知A、B、C三者的质量均为m=1kg,A、B与C间的动摩擦因数均为 ,C与地面间的动摩擦因数
,C与地面间的动摩擦因数 ,最大静摩擦力等于相应的滑动摩擦力,取重力加速度
,最大静摩擦力等于相应的滑动摩擦力,取重力加速度 。求:
。求:

 。
。 处的亮度为,在
处的亮度为,在 处取的一块小面积
处取的一块小面积 (虽然很小,但其尺度远大于条纹的细节)上未被条纹遮挡的部分的面积占比。
(虽然很小,但其尺度远大于条纹的细节)上未被条纹遮挡的部分的面积占比。 。量级
。量级 。
。 ,条纹的圆心在
,条纹的圆心在 。另一个光栅的条纹的宽度和条纹之间的间隙都为
。另一个光栅的条纹的宽度和条纹之间的间隙都为 ,条纹的圆心在
,条纹的圆心在 。将这两个光栅贴在一起后得到一个新的光栅。求均匀的平行光垂直通过这一光栅之后在光屏上得到的亮度分布
。将这两个光栅贴在一起后得到一个新的光栅。求均匀的平行光垂直通过这一光栅之后在光屏上得到的亮度分布 。量级
。量级 。
。 绕过其圆心的竖直轴匀速转动,将另一个半径为r,质量为m的小圆盘放在大圆盘上,小圆盘圆心与大圆盘圆心距离为
绕过其圆心的竖直轴匀速转动,将另一个半径为r,质量为m的小圆盘放在大圆盘上,小圆盘圆心与大圆盘圆心距离为 ,施加外力使得小圆盘圆心不动(外力不提供力矩)。求出稳定状态下,小圆盘的转动角速度。两盘间摩擦系数为
,施加外力使得小圆盘圆心不动(外力不提供力矩)。求出稳定状态下,小圆盘的转动角速度。两盘间摩擦系数为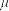
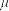 。圆筒由一根绳索牵引,绳索自由端速度为v。求出圆筒稳定运动时的质心速度和角速度。
。圆筒由一根绳索牵引,绳索自由端速度为v。求出圆筒稳定运动时的质心速度和角速度。  的斜坡上走路,
的斜坡上走路,  表示上坡,
表示上坡,  表示下坡。 高跷始终在与斜坡垂直的平面内运动。 将 Kat 视为质量为
表示下坡。 高跷始终在与斜坡垂直的平面内运动。 将 Kat 视为质量为  的质点, 将高跷视为轻硬细杆。 称杆的末端为“脚”。 每次开始迈步时, 斜坡给予后脚大小为
的质点, 将高跷视为轻硬细杆。 称杆的末端为“脚”。 每次开始迈步时, 斜坡给予后脚大小为  的瞬时冲量, 使这一结构从静止开始运动; 每次结束迈步时, 斜坡给予前脚一个瞬时冲量, 使这一结构静止。 每次迈步的过程中, 一只脚不与地面接触, 另一只脚始终与地面接触且不滑动 (即地面与脚之间的静摩擦系数
的瞬时冲量, 使这一结构从静止开始运动; 每次结束迈步时, 斜坡给予前脚一个瞬时冲量, 使这一结构静止。 每次迈步的过程中, 一只脚不与地面接触, 另一只脚始终与地面接触且不滑动 (即地面与脚之间的静摩擦系数 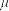 足够大)。 当脚与地面接触时, 其到 Kat 的距离保持为
足够大)。 当脚与地面接触时, 其到 Kat 的距离保持为  。 Kat 的步幅 (当两只脚同时与斜坡接触时它们之间的距离) 恒定为
。 Kat 的步幅 (当两只脚同时与斜坡接触时它们之间的距离) 恒定为 , 其中
, 其中 。
。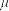 的范围。
的范围。 平面中, 求能让 Kat 按题目所说的方式走路的区域的面积。
平面中, 求能让 Kat 按题目所说的方式走路的区域的面积。 的比值, 用
的比值, 用 ,
, ,
, 表示,可以保留积分号。
表示,可以保留积分号。  的半径为
的半径为 的均匀的球形的黑体 A 放在一个半径为
的均匀的球形的黑体 A 放在一个半径为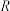 的均匀的薄球壳B内,两个球心的距离为
的均匀的薄球壳B内,两个球心的距离为 。在
。在 时,A 的温度为
时,A 的温度为 。A内部的热传导很快。
。A内部的热传导很快。 ,初始温度为
,初始温度为 的黑体。求
的黑体。求 时刻A的温度
时刻A的温度 。 (可保留代数方程, 积分,微分方程等,若数学计算过于复杂。)
。 (可保留代数方程, 积分,微分方程等,若数学计算过于复杂。) 时刻A的温度
时刻A的温度 。
。  的气体中有一单色平面纵波
的气体中有一单色平面纵波 。定义声压
。定义声压 是某一处压强对此处大气压强的偏离,声强很小时可认为
是某一处压强对此处大气压强的偏离,声强很小时可认为 ,其中c是气体中声波传播的速度。
,其中c是气体中声波传播的速度。 。
。 ,半径为
,半径为 的小球球心在声压场
的小球球心在声压场 处,求其受力,然后取
处,求其受力,然后取 近似,重解此问。
近似,重解此问。