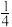 光滑圆弧的槽车(物块由皮带滑上槽车时无机械能损失).已知物体与皮带间的动摩擦因数为μ=0.8,求:
光滑圆弧的槽车(物块由皮带滑上槽车时无机械能损失).已知物体与皮带间的动摩擦因数为μ=0.8,求:
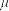 (
( )。一根长度为L、不可伸长的细线,一端固定于O′点,另一端系一质量为m0的小球Q。小球Q位于最低点时与物体P处于同一高度并恰好接触。现将小球Q拉至与O′同一高度(细线处于水平拉直状态),然后由静止释放,小球Q向下摆动并与物体P发生弹性碰撞(碰撞时间极短)。设物体P的质量为m,滑板的质量为2m。
)。一根长度为L、不可伸长的细线,一端固定于O′点,另一端系一质量为m0的小球Q。小球Q位于最低点时与物体P处于同一高度并恰好接触。现将小球Q拉至与O′同一高度(细线处于水平拉直状态),然后由静止释放,小球Q向下摆动并与物体P发生弹性碰撞(碰撞时间极短)。设物体P的质量为m,滑板的质量为2m。 的取值范围。
的取值范围。
 。直线NN'右侧有方向水平向左的电场(图中未画出),电场强度
。直线NN'右侧有方向水平向左的电场(图中未画出),电场强度 ,在包含圆弧轨道NP的ONO'P区域内有方向垂直纸面向外,磁感应强度为B的匀强磁场(边界处无磁场)。M点处静止一质量为m、电荷量为q的带负电物块A,一质量也为m的物块C从左侧以速度
,在包含圆弧轨道NP的ONO'P区域内有方向垂直纸面向外,磁感应强度为B的匀强磁场(边界处无磁场)。M点处静止一质量为m、电荷量为q的带负电物块A,一质量也为m的物块C从左侧以速度 撞向物块A,A、C之间的碰撞为弹性碰撞,A,C均可视为质点,与轨道MN的动摩擦因数为μ(μ未知),重力加速度为g,A在运动过程中所带电荷量保持不变且始终没有脱离轨道。求:
撞向物块A,A、C之间的碰撞为弹性碰撞,A,C均可视为质点,与轨道MN的动摩擦因数为μ(μ未知),重力加速度为g,A在运动过程中所带电荷量保持不变且始终没有脱离轨道。求: ,则A对轨道NP的最大压力大小。
,则A对轨道NP的最大压力大小。
 、
、 ,取重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8。求物块
,取重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8。求物块
 、方向相反.电场强度大小等于
、方向相反.电场强度大小等于 ,磁感应强度大小等于
,磁感应强度大小等于 ,求:(不计粒子重力,题中各物理量单位均为国际单位,计算结果可用分式表示)
,求:(不计粒子重力,题中各物理量单位均为国际单位,计算结果可用分式表示)
 m的立方体
m的立方体 ,以O为坐标原点,沿OA、
,以O为坐标原点,沿OA、 和OD方向分别建立x、y、z轴。在OACD面的中心M处存在一粒子发射源,可在底面内沿任意方向发射初速度为
和OD方向分别建立x、y、z轴。在OACD面的中心M处存在一粒子发射源,可在底面内沿任意方向发射初速度为 ,比荷
,比荷 的带正电粒子(不计重力)。可在区域内施加一定的匀强电场或者匀强磁场,使粒子可以到达相应的空间位置。
的带正电粒子(不计重力)。可在区域内施加一定的匀强电场或者匀强磁场,使粒子可以到达相应的空间位置。 面飞出,求施加电场的电场强度E的最小值;
面飞出,求施加电场的电场强度E的最小值; T,求粒子在磁场中运动时间的最大值
T,求粒子在磁场中运动时间的最大值 和最小值
和最小值 ;
; 。问(3)中最大时间和最小时间对应的粒子能否从
。问(3)中最大时间和最小时间对应的粒子能否从 面飞出?若粒子不能从
面飞出?若粒子不能从 面飞出,请写出这些粒子飞出立方体区域时的空间坐标(x,y,z)。
面飞出,请写出这些粒子飞出立方体区域时的空间坐标(x,y,z)。
 ,其中离子源紧贴小孔S;Ⅱ、Ⅲ区为长方体形状的磁偏转区,水平间距分别为d、
,其中离子源紧贴小孔S;Ⅱ、Ⅲ区为长方体形状的磁偏转区,水平间距分别为d、 ,其竖直截面与金属板形状相同。Ⅲ区左右截面的中心分别为
,其竖直截面与金属板形状相同。Ⅲ区左右截面的中心分别为 、
、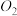 ,以
,以 为坐标原点,垂直长方体侧面和金属板建立x、y和z坐标轴。M、N间匀强电场大小为E,方向沿
为坐标原点,垂直长方体侧面和金属板建立x、y和z坐标轴。M、N间匀强电场大小为E,方向沿 方向;Ⅱ、Ⅲ区的匀强磁场大小相同、方向分别沿
方向;Ⅱ、Ⅲ区的匀强磁场大小相同、方向分别沿 、
、 方向。某时刻离子源有一电量为
方向。某时刻离子源有一电量为 、质量为m的粒子无初速的飘入小孔S,经过一段时间后恰好能返回到小孔S,不考虑粒子的重力。
、质量为m的粒子无初速的飘入小孔S,经过一段时间后恰好能返回到小孔S,不考虑粒子的重力。 方向增加一个附加匀强磁场,可使粒子经过小孔O后恰好不能进入到Ⅲ区、并直接从Ⅱ区前表面(
方向增加一个附加匀强磁场,可使粒子经过小孔O后恰好不能进入到Ⅲ区、并直接从Ⅱ区前表面( 方向一侧)P点飞出,求P点坐标为
方向一侧)P点飞出,求P点坐标为 。
。
 的液体表面上方有一单色激光发射器S,它能垂直液面射出细激光束,在液体内深h处水平放置一平面镜,镜面向上,平面镜中心O在光源S正下方。现让平面镜绕过O点垂直于纸面的轴开始逆时针匀速转动,转动周期为T,液面上方的观察者跟踪观察液面,观察到液面上有一光斑掠过,进一步观察发现光斑在液面上P、Q两位置间移动。下列说法正确的是( )
的液体表面上方有一单色激光发射器S,它能垂直液面射出细激光束,在液体内深h处水平放置一平面镜,镜面向上,平面镜中心O在光源S正下方。现让平面镜绕过O点垂直于纸面的轴开始逆时针匀速转动,转动周期为T,液面上方的观察者跟踪观察液面,观察到液面上有一光斑掠过,进一步观察发现光斑在液面上P、Q两位置间移动。下列说法正确的是( )
A.在平面镜开始转动的一个周期内,能观察到液面上光斑的时间为 |
B.液面上P、Q两位置间距离为 |
C.光斑刚要到达P点时的瞬时速度为 |
D.光斑由Q点运动到P点所用的时间为 |
 ,要使两小球保持相对静止,两小球A、B间的距离为( )
,要使两小球保持相对静止,两小球A、B间的距离为( )
| A.2L | B.3L | C. | D. |
 的初速度向右运动,与B发生弹性正碰。若重力加速度取
的初速度向右运动,与B发生弹性正碰。若重力加速度取 ,不考虑物块滑上传送带的能量损失。
,不考虑物块滑上传送带的能量损失。 ,求A落地时距离D点的水平距离;
,求A落地时距离D点的水平距离; ,
, ,B与传送带之间的动摩擦因数为
,B与传送带之间的动摩擦因数为 ,试求出物体B离开传送带时的动能
,试求出物体B离开传送带时的动能 与k的关系式。
与k的关系式。