全一卷
1.设集合 ,集合
,集合 ,则
,则
 ,集合
,集合 ,则
,则
A. | B. | C. | D. |
2.设 ,若
,若 ,
,
则 ()
()
 ,若
,若 ,
,则
 ()
()| A.-1 | B.0 | C.l | D.256 |
3.函数 的图像大致为.
的图像大致为.
 的图像大致为.
的图像大致为.A. | B. |
C. | D. |
4.设函数 .则
.则 值为 .
值为 .
 .则
.则 值为 .
值为 .A. | B.0 | C.1 | D.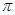 |
5.设正项等比数列 的前
的前 项和为且
项和为且 .则数列
.则数列 的公比为.
的公比为.
 的前
的前 项和为且
项和为且 .则数列
.则数列 的公比为.
的公比为.A. | B. | C. | D.1 |
6.某几何体的三视图如题(6)所示,其侧视图是一个边长为1的等边三角形,俯视图是两个正三角形拼成的菱形,则这个几何体的体积为


| A.1 | B. | C. | D. |
7.设变量 、
、 满足约束条件
满足约束条件 目标函数
目标函数 (
( 、
、 均大于0)的最大值为8.则
均大于0)的最大值为8.则 的最小值为.
的最小值为.
 、
、 满足约束条件
满足约束条件 目标函数
目标函数 (
( 、
、 均大于0)的最大值为8.则
均大于0)的最大值为8.则 的最小值为.
的最小值为.| A.3 | B.4 | C.5 | D.6 |
8.设  ,
, .则下面不等式中不恒成立的是.
.则下面不等式中不恒成立的是.
 ,
, .则下面不等式中不恒成立的是.
.则下面不等式中不恒成立的是.A. | B. |
C. | D. |
9.甲、乙两人玩猜数字游戏,先由甲心中想一个数字,记为 ,再由乙猜甲刚才所想的数字,把乙猜的数字记为
,再由乙猜甲刚才所想的数字,把乙猜的数字记为 ,其中,
,其中, 、
、 .若
.若 ,则称甲乙“心相近”.现任意找两人玩这个游戏,则它们心相近的概率为.
,则称甲乙“心相近”.现任意找两人玩这个游戏,则它们心相近的概率为.
 ,再由乙猜甲刚才所想的数字,把乙猜的数字记为
,再由乙猜甲刚才所想的数字,把乙猜的数字记为 ,其中,
,其中, 、
、 .若
.若 ,则称甲乙“心相近”.现任意找两人玩这个游戏,则它们心相近的概率为.
,则称甲乙“心相近”.现任意找两人玩这个游戏,则它们心相近的概率为.A. | B. | C. | D. |
10.设 是平面直角坐标系中两两不同的四点,若
是平面直角坐标系中两两不同的四点,若 ,
, ,且
,且 ,则称
,则称 调和分割
调和分割 .已知平面上的点
.已知平面上的点 调和分割点
调和分割点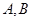 ,则下列说法正确的是
,则下列说法正确的是
 是平面直角坐标系中两两不同的四点,若
是平面直角坐标系中两两不同的四点,若 ,
, ,且
,且 ,则称
,则称 调和分割
调和分割 .已知平面上的点
.已知平面上的点 调和分割点
调和分割点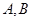 ,则下列说法正确的是
,则下列说法正确的是A. 可能线段 可能线段 的中点 的中点 |
B. 可能线段 可能线段 的中点 的中点 |
C. 可能同时在线段 可能同时在线段 上 上 |
D. 不可能同时在线段 不可能同时在线段 的延长线上 的延长线上 |
11.如图,在四棱锥 中,底面
中,底面 为正方形,边长为
为正方形,边长为 ,
, ,
, .若在此四棱锥中放入一个球,则球的的最大半径为.
.若在此四棱锥中放入一个球,则球的的最大半径为.

 中,底面
中,底面 为正方形,边长为
为正方形,边长为 ,
, ,
, .若在此四棱锥中放入一个球,则球的的最大半径为.
.若在此四棱锥中放入一个球,则球的的最大半径为.
A. | B. |
C. | D. |
12.设等差数列 满足:
满足: ,公差
,公差 .若当且仅当
.若当且仅当 时,数列
时,数列 的前
的前 项和
项和 取得最大值,则首项
取得最大值,则首项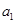 的取值范围是()
的取值范围是()
 满足:
满足: ,公差
,公差 .若当且仅当
.若当且仅当 时,数列
时,数列 的前
的前 项和
项和 取得最大值,则首项
取得最大值,则首项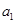 的取值范围是()
的取值范围是()A. | B. | C. | D. |
13.P为双曲线 右支上一点,M、N分别是圆
右支上一点,M、N分别是圆 上的点,则|PM|-|PN|的最大值为
上的点,则|PM|-|PN|的最大值为
 右支上一点,M、N分别是圆
右支上一点,M、N分别是圆 上的点,则|PM|-|PN|的最大值为
上的点,则|PM|-|PN|的最大值为 14.在 中,点O为BC的中点,过O的直线分别交直线AB,AC于不同的两点M,N若
中,点O为BC的中点,过O的直线分别交直线AB,AC于不同的两点M,N若 ,则
,则 的值为
的值为________

 中,点O为BC的中点,过O的直线分别交直线AB,AC于不同的两点M,N若
中,点O为BC的中点,过O的直线分别交直线AB,AC于不同的两点M,N若 ,则
,则 的值为
的值为
15.已知 ,
, ,且
,且 ,
, .则
.则 的值为_____________。
的值为_____________。
 ,
, ,且
,且 ,
, .则
.则 的值为_____________。
的值为_____________。16.若函数 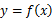 对定义域的每一个值
对定义域的每一个值 ,在其定义域内均存在唯一的
,在其定义域内均存在唯一的 ,满足
,满足 ,则称该函数为“依赖函数”。给出以下命题:
,则称该函数为“依赖函数”。给出以下命题:
① 为依赖函数;
为依赖函数;
② 为依赖函数;
为依赖函数;
③ 为依赖函数;
为依赖函数;
④ 为依赖函数;
为依赖函数;
⑤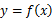 ,
,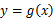 均为依赖函数,且定义域相同,则
均为依赖函数,且定义域相同,则 为依赖函数。
为依赖函数。
其中,所有真命题的序号为___________________。
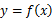 对定义域的每一个值
对定义域的每一个值 ,在其定义域内均存在唯一的
,在其定义域内均存在唯一的 ,满足
,满足 ,则称该函数为“依赖函数”。给出以下命题:
,则称该函数为“依赖函数”。给出以下命题:①
 为依赖函数;
为依赖函数;②
 为依赖函数;
为依赖函数;③
 为依赖函数;
为依赖函数;④
 为依赖函数;
为依赖函数;⑤
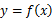 ,
,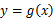 均为依赖函数,且定义域相同,则
均为依赖函数,且定义域相同,则 为依赖函数。
为依赖函数。其中,所有真命题的序号为___________________。
17.设函数 ,且
,且 ,
, .
.
(1)求 ,
, 的值;
的值;
(2)当 时,求
时,求 最大值.
最大值.
 ,且
,且 ,
, .
.(1)求
 ,
, 的值;
的值;(2)当
 时,求
时,求 最大值.
最大值.18.在一个盒子中,放有标号分别为1,2,3的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为x、y,设O为坐标原点,点P的坐标为 记
记 .
.
(1)求随机变量 的最大值,并求事件“
的最大值,并求事件“ 取得最大值”的概率;
取得最大值”的概率;
(2)求随机变量 的分布列和数学期望.
的分布列和数学期望.
 记
记 .
.(1)求随机变量
 的最大值,并求事件“
的最大值,并求事件“ 取得最大值”的概率;
取得最大值”的概率;(2)求随机变量
 的分布列和数学期望.
的分布列和数学期望.19.已知向量 ,
, ,其中,
,其中, .函数
.函数 的最小正周期为
的最小正周期为 .
.
(1)求 的值;
的值;
(2)设 的三边
的三边 、
、 、
、 满足
满足 ,且边
,且边 所对的角
所对的角 ,若关于
,若关于 的方程
的方程 有两个不同的实数解,求实数
有两个不同的实数解,求实数 的取值范围.
的取值范围.
 ,
, ,其中,
,其中, .函数
.函数 的最小正周期为
的最小正周期为 .
.(1)求
 的值;
的值;(2)设
 的三边
的三边 、
、 、
、 满足
满足 ,且边
,且边 所对的角
所对的角 ,若关于
,若关于 的方程
的方程 有两个不同的实数解,求实数
有两个不同的实数解,求实数 的取值范围.
的取值范围.20.如图所示的几何体中,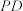 垂直于梯形
垂直于梯形 所在的平面,
所在的平面, 为
为 的中点,
的中点, ,四边形
,四边形 为矩形,线段
为矩形,线段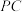 交
交 于点
于点 .
.

(1)求证: 平面
平面 ;
;
(2)求二面角 的正弦值;
的正弦值;
(3)在线段 上是否存在一点
上是否存在一点 ,使得
,使得 与平面
与平面 所成角的大小为
所成角的大小为 ?若存在,求出
?若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
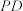 垂直于梯形
垂直于梯形 所在的平面,
所在的平面, 为
为 的中点,
的中点, ,四边形
,四边形 为矩形,线段
为矩形,线段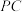 交
交 于点
于点 .
.
(1)求证:
 平面
平面 ;
;(2)求二面角
 的正弦值;
的正弦值;(3)在线段
 上是否存在一点
上是否存在一点 ,使得
,使得 与平面
与平面 所成角的大小为
所成角的大小为 ?若存在,求出
?若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.21.如图,椭圆
 的左焦点为
的左焦点为 ,过点
,过点 的直线交椭圆于
的直线交椭圆于 两点.
两点. 的最大值是
的最大值是 ,
, 的最小值是
的最小值是 ,满足
,满足 .
.
(1) 求该椭圆的离心率;
(2) 设线段 的中点为
的中点为 ,
, 的垂直平分线与
的垂直平分线与 轴和
轴和 轴分别交于
轴分别交于 两点,
两点, 是坐标原点.记
是坐标原点.记 的面积为
的面积为 ,
, 的面积为
的面积为 ,求
,求 的取值范围.
的取值范围.


 的左焦点为
的左焦点为 ,过点
,过点 的直线交椭圆于
的直线交椭圆于 两点.
两点. 的最大值是
的最大值是 ,
, 的最小值是
的最小值是 ,满足
,满足 .
.(1) 求该椭圆的离心率;
(2) 设线段
 的中点为
的中点为 ,
, 的垂直平分线与
的垂直平分线与 轴和
轴和 轴分别交于
轴分别交于 两点,
两点, 是坐标原点.记
是坐标原点.记 的面积为
的面积为 ,
, 的面积为
的面积为 ,求
,求 的取值范围.
的取值范围.
22.已知函数 .
.
(1)若函数 上是减函数,求实数a的最小值;
上是减函数,求实数a的最小值;
(2)若 ,使
,使 (
( )成立,求实数a的取值范围.
)成立,求实数a的取值范围.
 .
.(1)若函数
 上是减函数,求实数a的最小值;
上是减函数,求实数a的最小值;(2)若
 ,使
,使 (
( )成立,求实数a的取值范围.
)成立,求实数a的取值范围. 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错
