全一卷
1.若实数x、 满足
满足 ,则
,则 的最大值是
的最大值是________ .
 满足
满足 ,则
,则 的最大值是
的最大值是2.已知f(x)是R上最小正周期为2的周期函数,且当0≤x<2时,f(x)=x3-x,则函数y=f(x)的图象在区间[0,6]上与x轴的交点的个数为( ).
| A.6 | B.7 | C.8 | D.9 |
3.已知函数 ,
, ,若函数
,若函数 在区间
在区间 内单调递增,且函数
内单调递增,且函数 的图像关于直线
的图像关于直线 对称,则
对称,则 的值为
的值为________ .
 ,
, ,若函数
,若函数 在区间
在区间 内单调递增,且函数
内单调递增,且函数 的图像关于直线
的图像关于直线 对称,则
对称,则 的值为
的值为4.如图,a为程序框图中输出的结果.则二项式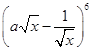 的展开式中含项的系数
的展开式中含项的系数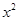 为___________.
为___________.
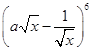 的展开式中含项的系数
的展开式中含项的系数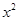 为___________.
为___________.
5.已知 .设C为直线OP上的一点(为为坐标原点).当
.设C为直线OP上的一点(为为坐标原点).当 取到最小值时,
取到最小值时, 的坐标为
的坐标为___________ .
 .设C为直线OP上的一点(为为坐标原点).当
.设C为直线OP上的一点(为为坐标原点).当 取到最小值时,
取到最小值时, 的坐标为
的坐标为6.已知奇函数 的定义域为
的定义域为 ,且在
,且在 内递减,求满足:
内递减,求满足: 的实数
的实数 的取值范围.
的取值范围.
 的定义域为
的定义域为 ,且在
,且在 内递减,求满足:
内递减,求满足: 的实数
的实数 的取值范围.
的取值范围.7.已知双曲线 的焦距为2c,直线l过点(a,0)、(b,0),且点(1,0)到直线l的距离与点(-1,0)到直线l的距离之和
的焦距为2c,直线l过点(a,0)、(b,0),且点(1,0)到直线l的距离与点(-1,0)到直线l的距离之和 .则双曲线离心率e的取值范围是__________.
.则双曲线离心率e的取值范围是__________.
 的焦距为2c,直线l过点(a,0)、(b,0),且点(1,0)到直线l的距离与点(-1,0)到直线l的距离之和
的焦距为2c,直线l过点(a,0)、(b,0),且点(1,0)到直线l的距离与点(-1,0)到直线l的距离之和 .则双曲线离心率e的取值范围是__________.
.则双曲线离心率e的取值范围是__________.8.已知甲、乙两个工程队各有若干人.若从甲工程队调90人到乙工程队,则乙工程队的总人数是甲工程队的2倍;若从乙工程队调部分人到甲工程队,则甲工程队的总人数是乙工程队的6倍.则甲工程队原来最少有__________人.
9.已知a、b为方程 的两个根.则
的两个根.则 __________.
__________.
 的两个根.则
的两个根.则 __________.
__________.10.数列 满足
满足 ,其中,
,其中,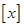 表示不超过实数x的最大整数,
表示不超过实数x的最大整数, .则
.则 __________.
__________.
 满足
满足 ,其中,
,其中,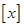 表示不超过实数x的最大整数,
表示不超过实数x的最大整数, .则
.则 __________.
__________.11.在非等腰 中,
中,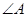 、
、 、
、 的对边分别为a、b、c,且满足
的对边分别为a、b、c,且满足 .
.
(1)求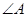 的大小;
的大小;
(2)若 ,求
,求 面积的取值范围.
面积的取值范围.
 中,
中,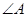 、
、 、
、 的对边分别为a、b、c,且满足
的对边分别为a、b、c,且满足 .
.(1)求
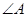 的大小;
的大小;(2)若
 ,求
,求 面积的取值范围.
面积的取值范围.12.在某电视娱乐节目的游戏活动中,每人需完成A、B、C三个项目.已知选手甲完成A、B、C三个项目的概率分别为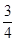 、
、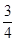 、
、 .每个项目之间相互独立.
.每个项目之间相互独立.
(1)选手甲对A、B、C三个项目各做一次,求甲至少完成一个项目的概率.
(2)该活动要求项目A、B 各做两次,项目C做三次.若两次项目A均完成,则进行项目B,并获得积分a;两次项目B均完成,则进行项目C,并获积分3a;三次项目C只要两次成功,则该选手闯关成功并获积分6a(积分不累计),且每个项目之间互相独立.用X表示选手甲所获积分的数值,写出X的分布列并求数学期望.
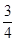 、
、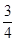 、
、 .每个项目之间相互独立.
.每个项目之间相互独立.(1)选手甲对A、B、C三个项目各做一次,求甲至少完成一个项目的概率.
(2)该活动要求项目A、B 各做两次,项目C做三次.若两次项目A均完成,则进行项目B,并获得积分a;两次项目B均完成,则进行项目C,并获积分3a;三次项目C只要两次成功,则该选手闯关成功并获积分6a(积分不累计),且每个项目之间互相独立.用X表示选手甲所获积分的数值,写出X的分布列并求数学期望.
13.如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,BC=CD=2,AC=4,∠ACB=∠ACD= ,F为PC的中点,AF⊥PB.
,F为PC的中点,AF⊥PB.
(1)求PA的长;
(2)求二面角B﹣AF﹣D的正弦值.

 ,F为PC的中点,AF⊥PB.
,F为PC的中点,AF⊥PB.(1)求PA的长;
(2)求二面角B﹣AF﹣D的正弦值.

14.设数列 的前n项和为
的前n项和为 ,点
,点 在
在 的图像上.
的图像上.
(1)求数列 的通项公式;
的通项公式;
(2)求 ,且对任意的正整数n,均有
,且对任意的正整数n,均有 .证明:对任意
.证明:对任意 ,总有
,总有 .
.
 的前n项和为
的前n项和为 ,点
,点 在
在 的图像上.
的图像上.(1)求数列
 的通项公式;
的通项公式;(2)求
 ,且对任意的正整数n,均有
,且对任意的正整数n,均有 .证明:对任意
.证明:对任意 ,总有
,总有 .
.15..
已知点 是椭圆
是椭圆 右焦点,点
右焦点,点 、
、 分别是x轴、 y上的动点,且满足
分别是x轴、 y上的动点,且满足 ,若点
,若点 满足
满足 .
.
(1)求 点的轨迹
点的轨迹 的方程;
的方程;
(2)设过点 任作一直线与点
任作一直线与点 的轨迹
的轨迹 交于
交于 、
、 两点,直线
两点,直线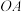 、
、 与直线
与直线 分别交于点
分别交于点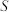 、
、 (其中
(其中 为坐标原点),试判断
为坐标原点),试判断 是否为定值?若是,求出这个定值;若不是,请说明理由.
是否为定值?若是,求出这个定值;若不是,请说明理由.
已知点
 是椭圆
是椭圆 右焦点,点
右焦点,点 、
、 分别是x轴、 y上的动点,且满足
分别是x轴、 y上的动点,且满足 ,若点
,若点 满足
满足 .
.(1)求
 点的轨迹
点的轨迹 的方程;
的方程;(2)设过点
 任作一直线与点
任作一直线与点 的轨迹
的轨迹 交于
交于 、
、 两点,直线
两点,直线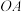 、
、 与直线
与直线 分别交于点
分别交于点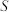 、
、 (其中
(其中 为坐标原点),试判断
为坐标原点),试判断 是否为定值?若是,求出这个定值;若不是,请说明理由.
是否为定值?若是,求出这个定值;若不是,请说明理由.16.已知函数 .
.
(1)设实数k使得 恒成立,求k的取值范围.
恒成立,求k的取值范围.
(2)设 .若函数
.若函数 在区间
在区间 内有两个零点,求k的取值范围.
内有两个零点,求k的取值范围.
 .
.(1)设实数k使得
 恒成立,求k的取值范围.
恒成立,求k的取值范围.(2)设
 .若函数
.若函数 在区间
在区间 内有两个零点,求k的取值范围.
内有两个零点,求k的取值范围. 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
