全一卷
1.设全集为R,集合 ,
, ,则
,则
 ,
, ,则
,则
A. | B. | C. | D. |
2.(2018年天津卷文)设变量x,y满足约束条件 则目标函数
则目标函数 的最大值为
的最大值为
 则目标函数
则目标函数 的最大值为
的最大值为| A.6 | B.19 | C.21 | D.45 |
3.阅读如图所示的程序框图,运行相应的程序,若输入 的值为20,则输出
的值为20,则输出 的值为
的值为

 的值为20,则输出
的值为20,则输出 的值为
的值为
| A.1 | B.2 | C.3 | D.4 |
4.设 ,则“
,则“ ”是“
”是“ ”的
”的
 ,则“
,则“ ”是“
”是“ ”的
”的| A.充分而不必要条件 |
| B.必要而不充分条件 |
| C.充要条件 |
| D.既不充分也不必要条件 |
5.已知 ,
, ,
, ,则a,b,c的大小关系为
,则a,b,c的大小关系为
 ,
, ,
, ,则a,b,c的大小关系为
,则a,b,c的大小关系为A. | B. | C. | D. |
6.将函数 的图象向右平移
的图象向右平移 个单位长度,所得图象对应的函数
个单位长度,所得图象对应的函数
 的图象向右平移
的图象向右平移 个单位长度,所得图象对应的函数
个单位长度,所得图象对应的函数A.在区间 上单调递增 上单调递增 | B.在区间 上单调递减 上单调递减 |
C.在区间 上单调递增 上单调递增 | D.在区间 上单调递减 上单调递减 |
7.已知双曲线 的离心率为2,过右焦点且垂直于
的离心率为2,过右焦点且垂直于 轴的直线与双曲线交于
轴的直线与双曲线交于 两点.设
两点.设 到双曲线的同一条渐近线的距离分别为
到双曲线的同一条渐近线的距离分别为 和
和 ,且
,且 则双曲线的方程为
则双曲线的方程为
 的离心率为2,过右焦点且垂直于
的离心率为2,过右焦点且垂直于 轴的直线与双曲线交于
轴的直线与双曲线交于 两点.设
两点.设 到双曲线的同一条渐近线的距离分别为
到双曲线的同一条渐近线的距离分别为 和
和 ,且
,且 则双曲线的方程为
则双曲线的方程为A. | B. |
C. | D. |
8.如图,在平面四边形ABCD中,
若点E为边CD上的动点,则 的最小值为
的最小值为


若点E为边CD上的动点,则
 的最小值为
的最小值为 
A. | B. | C. | D. |
9.i是虚数单位,复数
___________ .

10.在二项式 的展开式中,
的展开式中, 的系数为
的系数为__________ .
 的展开式中,
的展开式中, 的系数为
的系数为11.已知正方体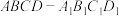 的棱长为1,除面
的棱长为1,除面 外,该正方体其余各面的中心分别为点E,F,G,H,M(如图),则四棱锥
外,该正方体其余各面的中心分别为点E,F,G,H,M(如图),则四棱锥 的体积为
的体积为__________ .

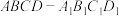 的棱长为1,除面
的棱长为1,除面 外,该正方体其余各面的中心分别为点E,F,G,H,M(如图),则四棱锥
外,该正方体其余各面的中心分别为点E,F,G,H,M(如图),则四棱锥 的体积为
的体积为
12.已知圆 的圆心为
的圆心为 ,直线
,直线 (
( 为参数)与该圆相交于
为参数)与该圆相交于 、
、 两点,则
两点,则 的面积为
的面积为___________ .
 的圆心为
的圆心为 ,直线
,直线 (
( 为参数)与该圆相交于
为参数)与该圆相交于 、
、 两点,则
两点,则 的面积为
的面积为13.已知 ,且
,且 ,则
,则 的最小值为
的最小值为_____________ .
 ,且
,且 ,则
,则 的最小值为
的最小值为14.已知 ,函数
,函数 若关于
若关于 的方程
的方程 恰有2个互异的实数解,则
恰有2个互异的实数解,则 的取值范围是
的取值范围是______________ .
 ,函数
,函数 若关于
若关于 的方程
的方程 恰有2个互异的实数解,则
恰有2个互异的实数解,则 的取值范围是
的取值范围是15.在 中,内角A,B,C所对的边分别为a,b,c.已知
中,内角A,B,C所对的边分别为a,b,c.已知 .
.
(1)求角B的大小;
(2)设a=2,c=3,求b和 的值.
的值.
 中,内角A,B,C所对的边分别为a,b,c.已知
中,内角A,B,C所对的边分别为a,b,c.已知 .
.(1)求角B的大小;
(2)设a=2,c=3,求b和
 的值.
的值.16.已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.
(I)应从甲、乙、丙三个部门的员工中分别抽取多少人?
(II)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.
(i)用X表示抽取的3人中睡眠不足 的员工人数,求随机变量X的分布列与数学期望;
(ii)设A为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A发生的概率.
(I)应从甲、乙、丙三个部门的员工中分别抽取多少人?
(II)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.
(i)用X表示抽取的3人中睡眠
(ii)设A为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A发生的概率.
17.如图, 且AD=2BC,
且AD=2BC, ,
, 且EG=AD,
且EG=AD, 且CD=2FG,
且CD=2FG, ,DA=DC=DG=2.
,DA=DC=DG=2.
(I)若M为CF的中点,N为EG的中点,求证: 平面
平面 ;
;
(II)求二面角 的正弦值;
的正弦值;
(III)若点P在线段DG上,且直线BP与平面ADGE所成的角为60°,求线段DP的长.

 且AD=2BC,
且AD=2BC, ,
, 且EG=AD,
且EG=AD, 且CD=2FG,
且CD=2FG, ,DA=DC=DG=2.
,DA=DC=DG=2.(I)若M为CF的中点,N为EG的中点,求证:
 平面
平面 ;
;(II)求二面角
 的正弦值;
的正弦值;(III)若点P在线段DG上,且直线BP与平面ADGE所成的角为60°,求线段DP的长.

18.设 是等比数列,公比大于0,其前n项和为
是等比数列,公比大于0,其前n项和为 ,
, 是等差数列.已知
是等差数列.已知 ,
, ,
, ,
, .
.
(I)求 和
和 的通项公式;
的通项公式;
(II)设数列 的前n项和为
的前n项和为 ,
,
(i)求 ;
;
(ii)证明 .
.
 是等比数列,公比大于0,其前n项和为
是等比数列,公比大于0,其前n项和为 ,
, 是等差数列.已知
是等差数列.已知 ,
, ,
, ,
, .
.(I)求
 和
和 的通项公式;
的通项公式;(II)设数列
 的前n项和为
的前n项和为 ,
,(i)求
 ;
;(ii)证明
 .
.19.设椭圆 (a>b>0)的左焦点为F,上顶点为B. 已知椭圆的离心率为
(a>b>0)的左焦点为F,上顶点为B. 已知椭圆的离心率为 ,点A的坐标为
,点A的坐标为 ,且
,且 .
.
(I)求椭圆的方程;
(II)设直线l: 与椭圆在第一象限的交点为P,且l与直线AB交于点Q. 若
与椭圆在第一象限的交点为P,且l与直线AB交于点Q. 若 (O为原点) ,求k的值.
(O为原点) ,求k的值.
 (a>b>0)的左焦点为F,上顶点为B. 已知椭圆的离心率为
(a>b>0)的左焦点为F,上顶点为B. 已知椭圆的离心率为 ,点A的坐标为
,点A的坐标为 ,且
,且 .
.(I)求椭圆的方程;
(II)设直线l:
 与椭圆在第一象限的交点为P,且l与直线AB交于点Q. 若
与椭圆在第一象限的交点为P,且l与直线AB交于点Q. 若 (O为原点) ,求k的值.
(O为原点) ,求k的值.20.已知函数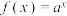 ,
, ,其中a>1.
,其中a>1.
(I)求函数 的单调区间;
的单调区间;
(II)若曲线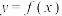 在点
在点 处的切线与曲线
处的切线与曲线 在点
在点 处的切线平行,证明:
处的切线平行,证明: ;
;
(III)证明:当 时,存在直线l,使l是曲线
时,存在直线l,使l是曲线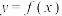 的切线,也是曲线
的切线,也是曲线 的切线.
的切线.
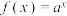 ,
, ,其中a>1.
,其中a>1.(I)求函数
 的单调区间;
的单调区间;(II)若曲线
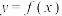 在点
在点 处的切线与曲线
处的切线与曲线 在点
在点 处的切线平行,证明:
处的切线平行,证明: ;
;(III)证明:当
 时,存在直线l,使l是曲线
时,存在直线l,使l是曲线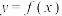 的切线,也是曲线
的切线,也是曲线 的切线.
的切线. 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错
