搜索
全一卷
难度系数：0.85 
答案解析
有奖纠错
1．如果将“收入50元”记作“+50元”，那么“支出20元”记作( )
| A．+20元 | B．﹣20元 | C．+30元 | D．﹣30元 |
2．下列几何体中，三视图的三个视图完全相同的几何体是( )
A． | B． |
C． | D． |
3．如图，平行线a，b被直线c所截，若∠1＝142°，则∠2的度数是( )
| A．142° | B．132° | C．58° | D．38° |
4．下列运算中，正确的是( )
| A．x2+x2＝x4 | B．3a3•2a2＝6a6 |
| C．6y6÷2y2＝3y3 | D．（﹣b2）3＝﹣b6 |
5．希望中学规定学生的学期体育成绩满分为100，其中体育课外活动占20%，期中考试成绩占30%，期末考试成绩占50%．若小强的三项成绩（百分制）依次是95，90，91．则小强这学期的体育成绩是( )
| A．92 | B．91.5 | C．91 | D．90 |
6．多项式
因式分解的结果是( )
因式分解的结果是( )| A．x（x﹣4）+4 | B．（x+2）（x﹣2） | C．（x+2）2 | D．（x﹣2）2 |
7．东东用仪器匀速向如图容器中注水，直到注满为止．用t表示注水时间，y表示水面的高度，下列图象适合表示y与t的对应关系的是( )
A． | B． | C． | D． |
8．如图，在菱形ABCD中，对角线AC，BD相交于点O，下列结论中错误的是( )
| A．AB＝AD | B．AC⊥BD | C．AC＝BD | D．∠DAC＝∠BAC |
9．如果点P（m，1+2m）在第三象限内，那么m的取值范围是( )
A． | B． | C． | D． |
10．如图，AB是⊙O的直径，PA与⊙O相切于点A，∠ABC＝25°，OC的延长线交PA于点P，则∠P的度数是( )
| A．25° | B．35° | C．40° | D．50° |
11．某厂家今年一月份的口罩产量是30万个，三月份的口罩产量是50万个，若设该厂家一月份到三月份的口罩产量的月平均增长率为x．则所列方程为( )
| A．30（1+x）2＝50 | B．30（1﹣x）2＝50 |
| C．30（1+x2）＝50 | D．30（1﹣x2）＝50 |
12．如图，在Rt△ABC中，
，
，
，将
绕点B顺时针旋转90°得到
．在此旋转过程中所扫过的面积为( )
，，，将绕点B顺时针旋转90°得到．在此旋转过程中所扫过的面积为( ) | A．25π+24 | B．5π+24 | C．25π | D．5π |
13．－2022的相反数是______ ．
14．若二次根式
有意义，则a的取值范围是 _____ ．
有意义，则a的取值范围是 15．如图，点P（x，y）在双曲线
的图象上，PA⊥x轴，垂足为A，若S△AOP＝2，则该反比例函数的解析式为 _____ ．
的图象上，PA⊥x轴，垂足为A，若S△AOP＝2，则该反比例函数的解析式为 16．如图，把边长为1：2的矩形ABCD沿长边BC，AD的中点E，F对折，得到四边形ABEF，点G，H分别在BE，EF上，且BG＝EH＝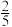
BE＝2，AG与BH交于点O，N为AF的中点，连接ON，作OM⊥ON交AB于点M，连接MN，则tan∠AMN＝_____ ．
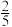BE＝2，AG与BH交于点O，N为AF的中点，连接ON，作OM⊥ON交AB于点M，连接MN，则tan∠AMN＝
17．计算：
．
．18．先化简,再求值
,其中
,其中
19．如图、在平面直角坐标系中，△ABC的三个顶点的坐标分别为A（4，1），B（2，3），C（1，2）．
(1)画出与△ABC关于y轴对称的△A1B1C1；
(2)以原点O为位似中心，在第三象限内画一个△A2B2C2，使它与△ABC的相似比为
，并写出点B2的坐标．
(1)画出与△ABC关于y轴对称的△A1B1C1；
(2)以原点O为位似中心，在第三象限内画一个△A2B2C2，使它与△ABC的相似比为
，并写出点B2的坐标．20．如图，点A，F，C，D在同一直线上，AB＝DE，AF＝CD，BC＝EF．
(1)求证：∠ACB＝∠DFE；
(2)连接BF，CE，直接判断四边形BFEC的形状．
(1)求证：∠ACB＝∠DFE；
(2)连接BF，CE，直接判断四边形BFEC的形状．
21．如图，小敏在数学实践活动中，利用所学知识对他所在小区居民楼AB的高度进行测量，从小敏家阳台C测得点A的仰角为33°，测得点B的俯角为45°，已知观测点到地面的高度CD＝36m，求居民楼AB的高度（结果保留整数．参考数据：sin33°≈0.55，cos33°≈0.84，tan33°≈0.65）．
22．为喜迎中国共产党第二十次全国代表大会的召开，红星中学举行党史知识竞赛．团委随机抽取了部分学生的成绩作为样本，把成绩按达标、良好、优秀、优异四个等级分别进行统计，并将所得数据绘制成如下不完整的统计图．
请根据图中提供的信息，解答下列问题：
(1)本次调查的样本容量是 ，圆心角β＝ 度；
(2)补全条形统计图；
(3)已知红星中学共有1200名学生，估计此次竞赛该校获优异等级的学生人数为多少？
(4)若在这次竞赛中有A，B，C，D四人成绩均为满分，现从中抽取2人代表学校参加县级比赛．请用列表或画树状图的方法求出恰好抽到A，C两人同时参赛的概率．
请根据图中提供的信息，解答下列问题：
(1)本次调查的样本容量是 ，圆心角β＝ 度；
(2)补全条形统计图；
(3)已知红星中学共有1200名学生，估计此次竞赛该校获优异等级的学生人数为多少？
(4)若在这次竞赛中有A，B，C，D四人成绩均为满分，现从中抽取2人代表学校参加县级比赛．请用列表或画树状图的方法求出恰好抽到A，C两人同时参赛的概率．
23．为改善村容村貌，阳光村计划购买一批桂花树和芒果树．已知桂花树的单价比芒果树的单价多40元，购买3棵桂花树和2棵芒果树共需370元．
(1)桂花树和芒果树的单价各是多少元？
(2)若该村一次性购买这两种树共60棵，且桂花树不少于35棵．设购买桂花树的棵数为n，总费用为w元，求w关于n的函数关系式，并求出该村按怎样的方案购买时，费用最低？最低费用为多少元？
(1)桂花树和芒果树的单价各是多少元？
(2)若该村一次性购买这两种树共60棵，且桂花树不少于35棵．设购买桂花树的棵数为n，总费用为w元，求w关于n的函数关系式，并求出该村按怎样的方案购买时，费用最低？最低费用为多少元？
24．如图，AB是⊙O的直径，E为⊙O上的一点，∠ABE的平分线交⊙O于点C，过点C的直线交BA的延长线于点P，交BE的延长线于点D．且∠PCA＝∠CBD．
(1)求证：PC为⊙O的切线；
(2)若PC＝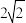
BO，PB＝12，求⊙O的半径及BE的长．
(1)求证：PC为⊙O的切线；
(2)若PC＝
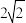BO，PB＝12，求⊙O的半径及BE的长．25．在平面直角坐标系中，抛物线L1：y＝ax2+2x+b与x轴交于两点A，B（3，0），与y轴交于点C（0，3）．
(1)求抛物线L1的函数解析式，并直接写出顶点D的坐标；
(2)如图，连接BD，若点E在线段BD上运动（不与B，D重合），过点E作EF⊥x轴于点F，设EF＝m，问：当m为何值时，△BFE与△DEC的面积之和最小；
(3)若将抛物线L1绕点B旋转180°得抛物线L2，其中C，D两点的对称点分别记作M，N．问：在抛物线L2的对称轴上是否存在点P，使得以B，M，P为顶点的三角形为等腰三角形？若存在，直接写出所有符合条件的点P的坐标；若不存在，请说明理由．
(1)求抛物线L1的函数解析式，并直接写出顶点D的坐标；
(2)如图，连接BD，若点E在线段BD上运动（不与B，D重合），过点E作EF⊥x轴于点F，设EF＝m，问：当m为何值时，△BFE与△DEC的面积之和最小；
(3)若将抛物线L1绕点B旋转180°得抛物线L2，其中C，D两点的对称点分别记作M，N．问：在抛物线L2的对称轴上是否存在点P，使得以B，M，P为顶点的三角形为等腰三角形？若存在，直接写出所有符合条件的点P的坐标；若不存在，请说明理由．
