 ,棒cd电阻为R,其余电阻不计。两棒最初静止,现给棒ab一个水平向右的瞬间冲量使得其获得初速度v0,已知棒cd到达MN前两棒不相碰且均已匀速。当棒cd刚进入区域Ⅱ时,对棒ab施加一水平向右的外力使棒ab向右做匀加速直线运动,外力随时间变化的图像如图乙所示。已知直线斜率为k,t0时刻棒cb恰好进入区域Ⅲ,棒cd进入区域Ⅲ后瞬间撤去棒ab上的外力。区域Ⅰ、Ⅲ导轨光滑,中间区域导轨粗糙且与棒cd的动摩擦因数为μ,两棒在运动过程中始终与导轨垂直且接触良好,棒ab始终在区域Ⅰ运动。已知
,棒cd电阻为R,其余电阻不计。两棒最初静止,现给棒ab一个水平向右的瞬间冲量使得其获得初速度v0,已知棒cd到达MN前两棒不相碰且均已匀速。当棒cd刚进入区域Ⅱ时,对棒ab施加一水平向右的外力使棒ab向右做匀加速直线运动,外力随时间变化的图像如图乙所示。已知直线斜率为k,t0时刻棒cb恰好进入区域Ⅲ,棒cd进入区域Ⅲ后瞬间撤去棒ab上的外力。区域Ⅰ、Ⅲ导轨光滑,中间区域导轨粗糙且与棒cd的动摩擦因数为μ,两棒在运动过程中始终与导轨垂直且接触良好,棒ab始终在区域Ⅰ运动。已知 ,
, ,重力加速度为g。求:
,重力加速度为g。求:

A. | B. |
C. | D. |
 ,x为弹簧的形变量。已知g=10m/s2,sin37°=0.6,cos37°=0.8。
,x为弹簧的形变量。已知g=10m/s2,sin37°=0.6,cos37°=0.8。
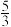 倍,产生的两列波在水面传播的速度均为2.0 m/s,其中S1产生波的波长为3 m。求:
倍,产生的两列波在水面传播的速度均为2.0 m/s,其中S1产生波的波长为3 m。求:
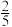 ,求电源内阻r.
,求电源内阻r.
 ,重力加速度为g,不计空气阻力。求:
,重力加速度为g,不计空气阻力。求:
 点,求初速度
点,求初速度 。
。
 若在交流电压变化的每个周期T内,平均产生320个上述微粒,试论证在t = 0到
若在交流电压变化的每个周期T内,平均产生320个上述微粒,试论证在t = 0到 这段时间内产生的微粒中,有多少微粒可到达A板(不计重力,不考虑微粒之间的相互作用)。
这段时间内产生的微粒中,有多少微粒可到达A板(不计重力,不考虑微粒之间的相互作用)。

| A.木板受到地面的摩擦力的大小一定是2μmg |
| B.木板受到地面的摩擦力的大小可能为3μmg |
C.当 时,木板P和木块Q一定发生相对运动 时,木板P和木块Q一定发生相对运动 |
| D.如果拉力F作用在木块Q上,无论怎样改变F的大小,木板都不可能运动 |
 。
。 ,速率变为原来的1%,则束流管的直径至少多大时才能收集到该类型的离子?
,速率变为原来的1%,则束流管的直径至少多大时才能收集到该类型的离子?