如图所示,一滑板的上表面由长度为
L的水平部分
AB和半径为
R的四分之一光滑圆弧
BC组成,两部分在
B点平滑连接,
A、
C为端点,滑板静止于光滑的水平地面上。物体P(视为质点)置于滑板上面的
A点,物体P与滑板水平部分
AB有摩擦。一长为
L不可伸长的细线,一端固定于
O′点,另一端系一质量为
m0的小球Q(视为质点),小球Q位于最低点时与物体P处于同一高度并恰好接触。现将小球Q拉至与
O′同一高度(细线处于水平拉直状态),然后由静止释放,小球Q向下摆动并与物体P发生弹性碰撞(碰撞时间极短)。已知物体P的质量为
m,滑板的质量为2
m,重力加速度大小为
g,cos5°
= 0.996,不计空气阻力。
(1)求小球Q与物体P碰撞后瞬间,物体P的速度大小;
(2)若要保证物体P能从
C点滑出,求物体P与滑板水平部分的动摩擦因数
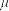
需满足的条件;
(3)若
m0= 1.5
m,
μ = 0.4,
R = 0.3
L,物体P在滑板上向左运动从
C点飞出,求飞出后相对
C点的最大高度;
(4)若
m0= 1.1
m,
μ = 0.4,小球Q与物体P发生弹性碰撞后,物体P将在滑板上向左运动,通过
B点后又返回,最终相对滑板静止于水平部分
AB上的某点,此时小球Q恰好是碰后第6次回到最低点。求物体P从第一次经过
B点到第二次经过
B点的时间。

 需满足的条件;
需满足的条件;
 ,其中m为振子质量,k为回复力系数。求:
,其中m为振子质量,k为回复力系数。求:
 的匀强电场及大小为B0的匀强磁场,让粒子对准I点并垂直平面MNN1M1入射,求粒子离开正方体区域时的坐标位置(结果可用根号和圆周率π表示)。
的匀强电场及大小为B0的匀强磁场,让粒子对准I点并垂直平面MNN1M1入射,求粒子离开正方体区域时的坐标位置(结果可用根号和圆周率π表示)。

 =1.05 ×10-34 J∙s)
=1.05 ×10-34 J∙s)  ,式中C为正的已知常量,l为该点到圆心O的距离。在y轴左侧,圆心为(-R,0)、半径为R的虚线圆内分布着方向垂直于圆面向外的匀强磁场,在x =-3R处有一竖直放置的足够长的荧光屏。今在x =2R圆弧的点放置一个粒子源,能不断释放质量为m、电荷量为q的粒子,粒子穿出磁场后偏转了60°,忽略粒子初速度,不计粒子重力和粒子间的相互作用力。
,式中C为正的已知常量,l为该点到圆心O的距离。在y轴左侧,圆心为(-R,0)、半径为R的虚线圆内分布着方向垂直于圆面向外的匀强磁场,在x =-3R处有一竖直放置的足够长的荧光屏。今在x =2R圆弧的点放置一个粒子源,能不断释放质量为m、电荷量为q的粒子,粒子穿出磁场后偏转了60°,忽略粒子初速度,不计粒子重力和粒子间的相互作用力。
 圆轨道平滑连接组成。一个质量为m的小球B静止在小车的左端。用一根不可伸长、长度为L轻质细绳悬挂一质量也为m的小球A,小球A静止时恰好和B接触,现将小球A向左拉到与悬点同一高度处(细线处于伸直状态)由静止释放,当小球A摆到最低点时与小球B刚好发生对心弹性碰撞,小球B水平冲上小车C恰好可以滑到轨道的最高点,(所有表面均光滑,A、B两小球半径r相等且r远小于L与R,B与C作用过程中没有机械能损失),求:
圆轨道平滑连接组成。一个质量为m的小球B静止在小车的左端。用一根不可伸长、长度为L轻质细绳悬挂一质量也为m的小球A,小球A静止时恰好和B接触,现将小球A向左拉到与悬点同一高度处(细线处于伸直状态)由静止释放,当小球A摆到最低点时与小球B刚好发生对心弹性碰撞,小球B水平冲上小车C恰好可以滑到轨道的最高点,(所有表面均光滑,A、B两小球半径r相等且r远小于L与R,B与C作用过程中没有机械能损失),求:
 ,此时物体B与地面刚好无压力。图中SD水平,位置R和Q关于S对称。现让小环从R处由静止释放,环下落过程中绳始终处于拉直状态,且环到达Q时速度最大。下列关于小环C下落过程中的描述正确的是( )
,此时物体B与地面刚好无压力。图中SD水平,位置R和Q关于S对称。现让小环从R处由静止释放,环下落过程中绳始终处于拉直状态,且环到达Q时速度最大。下列关于小环C下落过程中的描述正确的是( )
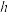 ,做匀速圆周运动的周期为T .已知月球半径为R ,引力常量为G.求:
,做匀速圆周运动的周期为T .已知月球半径为R ,引力常量为G.求: 的地方,将一质量为m的小球以v0的初速度水平抛出,求落地瞬间月球引力对小球做功的瞬时功率P.
的地方,将一质量为m的小球以v0的初速度水平抛出,求落地瞬间月球引力对小球做功的瞬时功率P. 
 ,内阻变大为r'=20Ω,某次开关接d时测得一电阻的读数为200Ω,则该电阻实际的阻值为
,内阻变大为r'=20Ω,某次开关接d时测得一电阻的读数为200Ω,则该电阻实际的阻值为