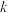 、自然长度均为0。两弹簧之间以一质量为
、自然长度均为0。两弹簧之间以一质量为 的小球相连。将弹簧1空着的一端悬挂于天花板上,整个系统自然下垂,初始时静止。已知两弹簧中任意一个一旦被拉伸至临界长度(该临界长度大于
的小球相连。将弹簧1空着的一端悬挂于天花板上,整个系统自然下垂,初始时静止。已知两弹簧中任意一个一旦被拉伸至临界长度(该临界长度大于 ,这里
,这里 表示重力加速度的大小)便会被拉断。
表示重力加速度的大小)便会被拉断。实验发现,如果缓慢地拉动下面的弹簧2的下端,上面的弹簧1将被拉断。如果快速地拉动,则很有可能拉断下面的弹簧2。
(1)设加载于弹簧2下端的作用力随时间变化的关系为
 ,写出弹簧1的长度
,写出弹簧1的长度 及小球加速度
及小球加速度 所满足的运动方程。
所满足的运动方程。(2)在一个简单模型中,假设
 与时间
与时间 的关系为
的关系为
其中
 为大于零的常量,它的大小对应力加载的快慢。求在该力的作用下弹簧1、2在
为大于零的常量,它的大小对应力加载的快慢。求在该力的作用下弹簧1、2在 (
( )时刻的长度
)时刻的长度 、
、 。
。(3)记某一弹簧先被拉断的时刻为
 ,根据(2)中的结果,
,根据(2)中的结果,(ⅰ)求使弹簧1必然先被拉断所对应的
 取值范围;
取值范围;(ⅱ)对于并非必然使弹簧1先被拉断的
 取值,分析使弹簧1先被拉断的时刻
取值,分析使弹簧1先被拉断的时刻 需满足的条件(表达式中可含有
需满足的条件(表达式中可含有 );
);(ⅲ)求弹簧2先被拉断的可能性与
 取值大小的关系,并用此关系说明题述实验现象。
取值大小的关系,并用此关系说明题述实验现象。(4)给定临界长度为
 ,要确保弹簧2先被拉断,试确定
,要确保弹簧2先被拉断,试确定 需满足的关系式。有无可能两弹簧同时被拉断?若有,试求出能让两弹簧同时达到临界长度
需满足的关系式。有无可能两弹簧同时被拉断?若有,试求出能让两弹簧同时达到临界长度 所对应的
所对应的 满足的关系式。
满足的关系式。
同类型试题

y = sin x, x∈R, y∈[–1,1],周期为2π,函数图像以 x = (π/2) + kπ 为对称轴
y = arcsin x, x∈[–1,1], y∈[–π/2,π/2]
sin x = 0 ←→ arcsin x = 0
sin x = 1/2 ←→ arcsin x = π/6
sin x = √2/2 ←→ arcsin x = π/4
sin x = 1 ←→ arcsin x = π/2
y = sin x, x∈R, y∈[–1,1],周期为2π,函数图像以 x = (π/2) + kπ 为对称轴
y = arcsin x, x∈[–1,1], y∈[–π/2,π/2]
sin x = 0 ←→ arcsin x = 0
sin x = 1/2 ←→ arcsin x = π/6
sin x = √2/2 ←→ arcsin x = π/4
sin x = 1 ←→ arcsin x = π/2
 搜索
搜索

