搜索
，D为线段AB上的动点，连接DC，将DC绕点D顺时针旋转得到DE，连接CE，BE．
（1）如图1，当
＝60°时，求证：△CAD≌△CBE；（2）如图2，当tanα＝
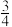时，①探究AD和BE之间的数量关系，并说明理由；
②若AC＝5，H是BC上一点，在点D移动过程中，CE＋EH是否存在最小值？若存在，请直接写出CE＋EH的最小值；若不存在，请说明理由．
同类型试题
y = sin x， x∈R， y∈[–1，1]，周期为2π，函数图像以 x = (π/2) + kπ 为对称轴
y = arcsin x， x∈[–1，1]， y∈[–π/2，π/2]
sin x = 0 ←→ arcsin x = 0
sin x = 1/2 ←→ arcsin x = π/6
sin x = √2/2 ←→ arcsin x = π/4
sin x = 1 ←→ arcsin x = π/2
y = sin x， x∈R， y∈[–1，1]，周期为2π，函数图像以 x = (π/2) + kπ 为对称轴
y = arcsin x， x∈[–1，1]， y∈[–π/2，π/2]
sin x = 0 ←→ arcsin x = 0
sin x = 1/2 ←→ arcsin x = π/6
sin x = √2/2 ←→ arcsin x = π/4
sin x = 1 ←→ arcsin x = π/2
