搜索
），抛物线与轴的一个交点为A（4，0），点B（2，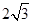
）
（1）判断点C是否在该抛物线上，并说明理由；
（2）顺次连接AB，BC，CO；
（3）设点P是抛物线上的动点，连接PM、PC、AC，△PAC的面积S随点P的运动而变化；当S的值为②时，求点P的横坐标的值．
| 直线AC的 函数表达式 | S取的一 个特殊值 | 满足条件的 P点的个数 | S的可能 取值范围 |
| ① | | | |
| 6 | 4个 | ③ | |
| ② | 3个 | | |
| 10 | 2个 | ④ | |
同类型试题
y = sin x， x∈R， y∈[–1，1]，周期为2π，函数图像以 x = (π/2) + kπ 为对称轴
y = arcsin x， x∈[–1，1]， y∈[–π/2，π/2]
sin x = 0 ←→ arcsin x = 0
sin x = 1/2 ←→ arcsin x = π/6
sin x = √2/2 ←→ arcsin x = π/4
sin x = 1 ←→ arcsin x = π/2
y = sin x， x∈R， y∈[–1，1]，周期为2π，函数图像以 x = (π/2) + kπ 为对称轴
y = arcsin x， x∈[–1，1]， y∈[–π/2，π/2]
sin x = 0 ←→ arcsin x = 0
sin x = 1/2 ←→ arcsin x = π/6
sin x = √2/2 ←→ arcsin x = π/4
sin x = 1 ←→ arcsin x = π/2
