搜索
材料一：若三个非零实数x，y，z满足：只要其中一个数的倒数等于另外两个数的倒数的和，则称这三个实数x，y，z构成“和谐三数组”.
材料二：若关于x的一元二次方程ax2+bx +c= 0(a≠0)的两根分别为
，
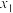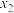，则有
，
．问题解决：
（1）请你写出三个能构成“和谐三数组”的实数 ；
（2）若
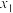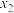，是关于x的方程ax2+bx +c= 0 (a，b，c均不为0)的两根，
是关于x的方程bx+c=0(b，c均不为0)的解．求证：x1，x2，x3可以构成“和谐三数组”；（3）若A(m，y1) ，B(m + 1，y2) ，C(m+3，y3)三个点均在反比例函数
的图象上，且三点的纵坐标恰好构成“和谐三数组”，求实数m的值．
同类型试题
y = sin x， x∈R， y∈[–1，1]，周期为2π，函数图像以 x = (π/2) + kπ 为对称轴
y = arcsin x， x∈[–1，1]， y∈[–π/2，π/2]
sin x = 0 ←→ arcsin x = 0
sin x = 1/2 ←→ arcsin x = π/6
sin x = √2/2 ←→ arcsin x = π/4
sin x = 1 ←→ arcsin x = π/2
y = sin x， x∈R， y∈[–1，1]，周期为2π，函数图像以 x = (π/2) + kπ 为对称轴
y = arcsin x， x∈[–1，1]， y∈[–π/2，π/2]
sin x = 0 ←→ arcsin x = 0
sin x = 1/2 ←→ arcsin x = π/6
sin x = √2/2 ←→ arcsin x = π/4
sin x = 1 ←→ arcsin x = π/2
