全一卷
1.化简 的值是( )
的值是( )
 的值是( )
的值是( )A. | B.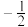 | C. | D. |
2.函数 的图象是( )
的图象是( )
 的图象是( )
的图象是( )A. | B. |
C. | D. |
3.已知直线 和圆
和圆 相切,那么a的值是( )
相切,那么a的值是( )
 和圆
和圆 相切,那么a的值是( )
相切,那么a的值是( )| A.5 | B.4 | C.3 | D.2 |
4.两条直线 垂直的充要条件是( )
垂直的充要条件是( )
 垂直的充要条件是( )
垂直的充要条件是( )A. | B. |
C. | D. |
5.函数 的反函数
的反函数 ( )
( )
 的反函数
的反函数 ( )
( )A. | B. |
C. | D. |
6.已知点 在第一象限,则在
在第一象限,则在 内
内 的取值范围是( ).
的取值范围是( ).
 在第一象限,则在
在第一象限,则在 内
内 的取值范围是( ).
的取值范围是( ).A. | B. |
C. | D. |
7.已知圆锥的全面积是底面积的3倍,那么该圆锥的侧面展开图扇形的圆心角为( )
A. | B. | C. | D. |
8.复数-i的一个立方根是i,它的另外两个立方根是( )
A. | B. | C. | D. |
9.如果棱台的两底面积分别是S,S′,中截面的面积是S0,那么
A.2 = = + + | B.S0= |
| C.2S0=S+S′ | D.S0=2S′S |
10.2名医生和4名护士被分配到2所学校为学生体检,每校分配1名医生和2名护士,不同的分配方法共有( )
| A.6种 | B.12种 | C.18种 | D.24种 |
11.向高为H的水瓶内注水,一直到注满为止,如果注水量V与水深h的函数图象如图所示,那么水瓶的形状大致是( )


A. | B. | C. | D. |
12.椭圆 =1的焦点为F1和F2,点P在椭圆上,如果线段PF1的中点在y轴上,那么|PF1|是|PF2|的( )
=1的焦点为F1和F2,点P在椭圆上,如果线段PF1的中点在y轴上,那么|PF1|是|PF2|的( )
 =1的焦点为F1和F2,点P在椭圆上,如果线段PF1的中点在y轴上,那么|PF1|是|PF2|的( )
=1的焦点为F1和F2,点P在椭圆上,如果线段PF1的中点在y轴上,那么|PF1|是|PF2|的( )| A.7倍 | B.5倍 | C.4倍 | D.3倍 |
13.球面上有3个点,其中任意两点的球面距离都等于大圆周长的 ,经过这3个点的小圆的周长为
,经过这3个点的小圆的周长为 ,那么这个球的半径为( )
,那么这个球的半径为( )
 ,经过这3个点的小圆的周长为
,经过这3个点的小圆的周长为 ,那么这个球的半径为( )
,那么这个球的半径为( )A. | B.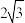 | C. | D. |
14.一个直角三角形三内角的正弦值成等比数列,其最小内角的正弦值为( )
A. | B. | C. | D. |
15.等比数列 的公比为
的公比为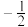 ,前n项和为
,前n项和为 ,满足
,满足 ,那么
,那么 的值为( )
的值为( )
 的公比为
的公比为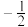 ,前n项和为
,前n项和为 ,满足
,满足 ,那么
,那么 的值为( )
的值为( )A. | B. | C. | D. |
16.已知圆C过双曲线 的一个顶点和一个焦点,且圆心在此双曲线上,则圆心到双曲线中心的距离是
的一个顶点和一个焦点,且圆心在此双曲线上,则圆心到双曲线中心的距离是________ .
 的一个顶点和一个焦点,且圆心在此双曲线上,则圆心到双曲线中心的距离是
的一个顶点和一个焦点,且圆心在此双曲线上,则圆心到双曲线中心的距离是17. 的展开式中x的系数为
的展开式中x的系数为_____________ .(用数字作答)
 的展开式中x的系数为
的展开式中x的系数为18.如图所示,在直四棱柱 中,当底面四边形ABCD满足条件
中,当底面四边形ABCD满足条件________ 时,有A1C⊥B1D1(注:填上你认为正确的一个条件即可,不必考虑所有可能的情形).

 中,当底面四边形ABCD满足条件
中,当底面四边形ABCD满足条件
19.关于函数 ,有下列命题:
,有下列命题:
①由 可得
可得 必是
必是 的整数倍;
的整数倍;
② 的表达式可改写为
的表达式可改写为 ;
;
③ 的图象关于点
的图象关于点 对称;
对称;
④ 的图象关于直线
的图象关于直线 对称.
对称.
其中正确的命题的序号是_____________ .(注:把你认为正确的命题的序号都填上)
 ,有下列命题:
,有下列命题:①由
 可得
可得 必是
必是 的整数倍;
的整数倍;②
 的表达式可改写为
的表达式可改写为 ;
;③
 的图象关于点
的图象关于点 对称;
对称;④
 的图象关于直线
的图象关于直线 对称.
对称.其中正确的命题的序号是
20.设a≠b,解关于x的不等式a2x+b2(1-x)≥[ax+b(1-x)]2.
21.在△ABC中,a,b,c分别是角A,B,C的对边,设 ,求sinB的值.
,求sinB的值.
 ,求sinB的值.
,求sinB的值.22.如图,直线l1和l2相交于点M,l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若 AMN为锐角三角形,|AM|=
AMN为锐角三角形,|AM|= ,|AN|=3,且|BN|=6.建立适当的坐标系,求曲线段C的方程.
,|AN|=3,且|BN|=6.建立适当的坐标系,求曲线段C的方程.

 AMN为锐角三角形,|AM|=
AMN为锐角三角形,|AM|= ,|AN|=3,且|BN|=6.建立适当的坐标系,求曲线段C的方程.
,|AN|=3,且|BN|=6.建立适当的坐标系,求曲线段C的方程.
23.已知斜三棱柱 的侧面
的侧面 与底面
与底面 垂直,
垂直, ,且
,且 .
.

(1)求侧棱 与底面
与底面 所成角的大小;
所成角的大小;
(2)求侧面 与底面
与底面 所成二面角的大小;
所成二面角的大小;
(3)求侧棱 和侧面
和侧面 的距离.
的距离.
 的侧面
的侧面 与底面
与底面 垂直,
垂直, ,且
,且 .
.
(1)求侧棱
 与底面
与底面 所成角的大小;
所成角的大小;(2)求侧面
 与底面
与底面 所成二面角的大小;
所成二面角的大小;(3)求侧棱
 和侧面
和侧面 的距离.
的距离.24.如图所示,为处理含有某种杂质的污水,要制造一底宽为2米的无盖长方体沉淀箱,污水从A孔流入,经沉淀后从B孔流出,设箱体的长度为a米,高度为b米.已知流出的水中该杂质的质量分数与a、b的乘积ab成反比.现有制箱材料60平方米.问当a、b各为多少米时,经沉淀后流出的水中该杂质的质量分数最小(A、B孔的面积忽略不计)?


25.已知数列{bn}是等差数列,b1=1,b1+b2+…+b10=145.
(1)求数列{bn}的通项公式bn;
(2)设数列{an}的通项an=loga (其中a>0且a≠1).记Sn是数列{an}的前n项和,试比较Sn与
(其中a>0且a≠1).记Sn是数列{an}的前n项和,试比较Sn与 logabn+1的大小,并证明你的结论.
logabn+1的大小,并证明你的结论.
(1)求数列{bn}的通项公式bn;
(2)设数列{an}的通项an=loga
 (其中a>0且a≠1).记Sn是数列{an}的前n项和,试比较Sn与
(其中a>0且a≠1).记Sn是数列{an}的前n项和,试比较Sn与 logabn+1的大小,并证明你的结论.
logabn+1的大小,并证明你的结论. 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
