全一卷
1.假设集合 ,
,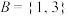 ,那么
,那么 等于( )
等于( )
 ,
,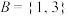 ,那么
,那么 等于( )
等于( )A. | B. | C. | D. |
2. 的解集是( )
的解集是( )
 的解集是( )
的解集是( )A. | B. |
C. | D. |
3.函数 的定义域为( )
的定义域为( )
 的定义域为( )
的定义域为( )A. 且 且 | B. |
C. 且 且 | D. |
4.“圆心到直线的距离等于圆的半径”是“直线与圆相切”的( )
| A.充分没必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也没必要条件 |
5.在等比数列 中,
中,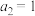 ,
, ,则
,则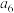 等于( )
等于( )
 中,
中,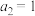 ,
, ,则
,则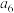 等于( )
等于( )A. | B.5 | C. | D.9 |
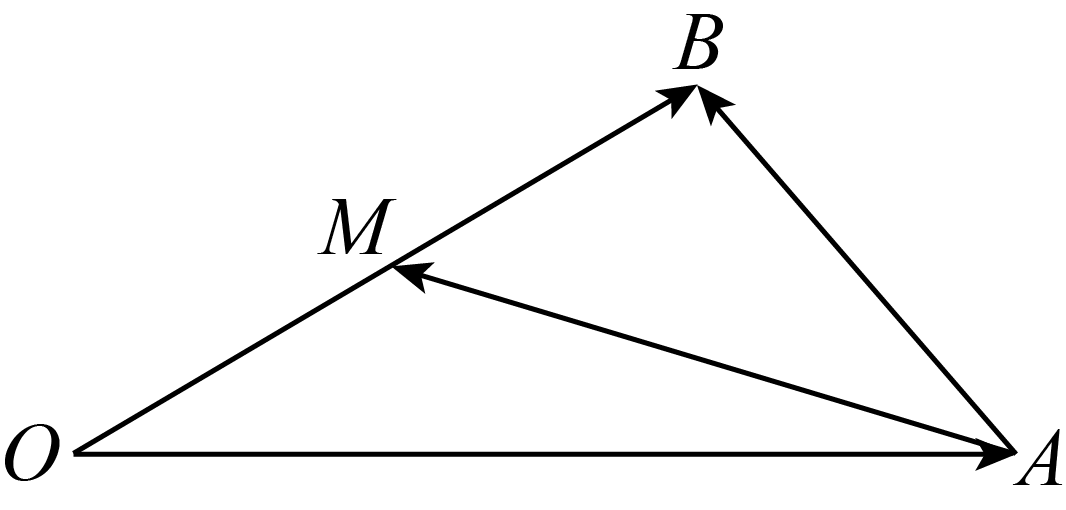
6.如下图, 是线段
是线段 的中点,设向量
的中点,设向量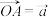 ,
, ,那么
,那么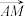 能够表示为( )
能够表示为( )
 是线段
是线段 的中点,设向量
的中点,设向量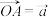 ,
, ,那么
,那么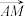 能够表示为( )
能够表示为( )
A. | B. |
C. | D. |
7.终边在 轴的正半轴上的角的集合是( )
轴的正半轴上的角的集合是( )
 轴的正半轴上的角的集合是( )
轴的正半轴上的角的集合是( )A. | B. |
C. | D. |
8.关于函数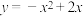 ,以下表达错误的选项是( )
,以下表达错误的选项是( )
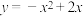 ,以下表达错误的选项是( )
,以下表达错误的选项是( )| A.函数的最大值是1 | B.函数图象的对称轴是直线 |
C.函数的单调递减区间是 | D.函数图象过点 |
9.某值日小组共有5名同窗,假设任意安排3名同窗负责教室内的地面卫生,其余2名同窗负责教室外的走廊卫生,那么不同的安排方式种数是( )
| A.10 | B.20 | C.60 | D.100 |
10.如下图,直线 的方程是( )
的方程是( )

 的方程是( )
的方程是( )
A. | B. |
C. | D. |
11.关于命题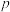 ,
, ,假设“
,假设“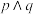 为假命题”,且
为假命题”,且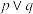 为真命题,那么( )
为真命题,那么( )
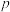 ,
, ,假设“
,假设“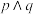 为假命题”,且
为假命题”,且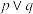 为真命题,那么( )
为真命题,那么( )A.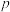 , , 都是真命题 都是真命题 | B.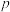 , , 都是假命题 都是假命题 |
C.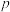 , , 一个是真命题一个是假命题 一个是真命题一个是假命题 | D.无法判定 |
12.已知函数 是奇函数,当
是奇函数,当 时,
时, ,那么
,那么 的值是( )
的值是( )
 是奇函数,当
是奇函数,当 时,
时, ,那么
,那么 的值是( )
的值是( )A. | B. | C.1 | D.3 |
13.已知点 在函数
在函数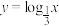 的图象上,点
的图象上,点 的坐标是
的坐标是 ,那么
,那么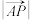 的值是( )
的值是( )
 在函数
在函数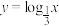 的图象上,点
的图象上,点 的坐标是
的坐标是 ,那么
,那么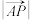 的值是( )
的值是( )A. | B. | C. | D. |
14.关于 ,
, 的方程
的方程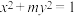 ,给出以下命题;
,给出以下命题;
①当 时,方程表示双曲线;②当
时,方程表示双曲线;②当 时,方程表示抛物线;③当
时,方程表示抛物线;③当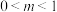 时,方程表示椭圆;④当
时,方程表示椭圆;④当 时,方程表示等轴双曲线;⑤当
时,方程表示等轴双曲线;⑤当 时,方程表示椭圆.
时,方程表示椭圆.
其中,真命题的个数是( )
 ,
, 的方程
的方程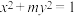 ,给出以下命题;
,给出以下命题;①当
 时,方程表示双曲线;②当
时,方程表示双曲线;②当 时,方程表示抛物线;③当
时,方程表示抛物线;③当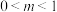 时,方程表示椭圆;④当
时,方程表示椭圆;④当 时,方程表示等轴双曲线;⑤当
时,方程表示等轴双曲线;⑤当 时,方程表示椭圆.
时,方程表示椭圆.其中,真命题的个数是( )
| A.2 | B.3 | C.4 | D.5 |
15. 的二项展开式中,所有项的二项式系数之和是( )
的二项展开式中,所有项的二项式系数之和是( )
 的二项展开式中,所有项的二项式系数之和是( )
的二项展开式中,所有项的二项式系数之和是( )| A.0 | B. | C. | D.32 |
16.不等式组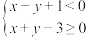 表示的区域(阴影部分)是( )
表示的区域(阴影部分)是( )
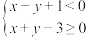 表示的区域(阴影部分)是( )
表示的区域(阴影部分)是( )A. | B. |
C. | D. |
17.甲、乙、丙三位同窗打算利用假期外出游览,约定每人从泰山、孔府这两处景点中任选一处,那么甲、乙两位同学恰好选取同一处景点的概率是( )
A. | B. | C. | D. |
18.已知向量 ,
, ,那么
,那么 等于( )
等于( )
 ,
, ,那么
,那么 等于( )
等于( )A. | B. | C.1 | D.0 |
19.已知 ,
,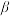 表示平面,
表示平面, ,
, 表示直线,以下命题中正确的选项是( )
表示直线,以下命题中正确的选项是( )
 ,
,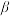 表示平面,
表示平面, ,
, 表示直线,以下命题中正确的选项是( )
表示直线,以下命题中正确的选项是( )A.假设 , , ,那么 ,那么 |
B.假设 , , , , ,那么 ,那么 |
C.假设 , , ,那么 ,那么 |
D.假设 , , , , , , ,那么 ,那么 |
20.已知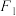 是双曲线
是双曲线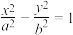 (
( ,
, )的左焦点,点
)的左焦点,点 在双曲线上,直线
在双曲线上,直线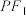 与
与 轴垂直,且
轴垂直,且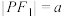 ,那么双曲线的离心率是( )
,那么双曲线的离心率是( )
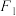 是双曲线
是双曲线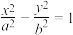 (
( ,
, )的左焦点,点
)的左焦点,点 在双曲线上,直线
在双曲线上,直线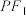 与
与 轴垂直,且
轴垂直,且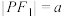 ,那么双曲线的离心率是( )
,那么双曲线的离心率是( )A. | B. | C.2 | D.3 |
21.直棱柱的底面是边长为 的菱形,侧棱长为
的菱形,侧棱长为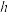 ,那么直棱柱的侧面积是
,那么直棱柱的侧面积是______ .
 的菱形,侧棱长为
的菱形,侧棱长为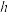 ,那么直棱柱的侧面积是
,那么直棱柱的侧面积是22.在△ 中,
中,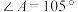 ,
, ,
, ,
, 等于
等于______ .
 中,
中,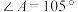 ,
, ,
, ,
, 等于
等于23.打算从500名学生中抽取50名进行问卷调查,拟采纳系统抽样方式,为此将他们一一编号为1~500,并对编号进行分段,假设从第一个号码段中随机抽出的号码是2,那么从第五个号码段中抽出的号码应是______ .
24.已知椭圆的中心在坐标原点,右焦点与圆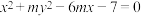 的圆心重合,长轴长等于圆的直径,那么短轴长等于
的圆心重合,长轴长等于圆的直径,那么短轴长等于______ .
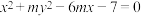 的圆心重合,长轴长等于圆的直径,那么短轴长等于
的圆心重合,长轴长等于圆的直径,那么短轴长等于25.集合 ,
, ,
,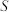 都是非空集合,现规定如下运算:
都是非空集合,现规定如下运算: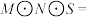
 且
且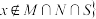 .假设集合
.假设集合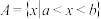 ,
,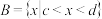 ,
,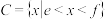 ,其中实数
,其中实数 ,
, ,
, ,
,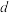 ,
, ,
,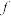 满足:(1)
满足:(1)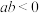 ,
, ;
;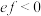 ;(2)
;(2) ;(3)
;(3) .计算
.计算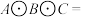
____________________________________ .
 ,
, ,
,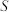 都是非空集合,现规定如下运算:
都是非空集合,现规定如下运算: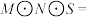
 且
且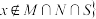 .假设集合
.假设集合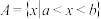 ,
,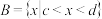 ,
,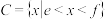 ,其中实数
,其中实数 ,
, ,
, ,
,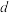 ,
, ,
,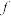 满足:(1)
满足:(1)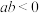 ,
, ;
;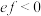 ;(2)
;(2) ;(3)
;(3) .计算
.计算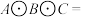
26.某学校合唱团参加演出,需要把120名演员排成5排,而且从第二排起,每排比前一排多3名,求第一排应安排多少名演员.
27.已知函数 ,
, ,
,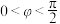 ,函数的部分图象如下图,求
,函数的部分图象如下图,求
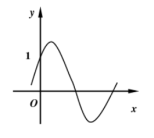
(1)函数的最小正周期 及
及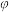 的值:
的值:
(2)函数的单调递增区间.
 ,
, ,
,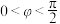 ,函数的部分图象如下图,求
,函数的部分图象如下图,求
(1)函数的最小正周期
 及
及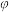 的值:
的值:(2)函数的单调递增区间.
28.已知函数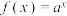 (
( 且
且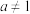 )在区间
)在区间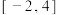 上的最大值是16,
上的最大值是16,
(1)求实数 的值;
的值;
(2)假设函数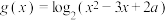 的定义域是
的定义域是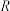 ,求不等式
,求不等式 的实数
的实数 的取值范围.
的取值范围.
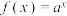 (
( 且
且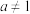 )在区间
)在区间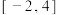 上的最大值是16,
上的最大值是16,(1)求实数
 的值;
的值;(2)假设函数
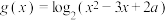 的定义域是
的定义域是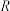 ,求不等式
,求不等式 的实数
的实数 的取值范围.
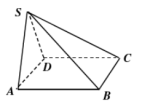
的取值范围.29.如下图,在四棱锥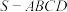 中,底面
中,底面 是正方形,平面
是正方形,平面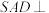 平面
平面 ,
,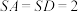 ,
,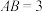 .
.
(1)求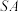 与
与 所成角的余弦值;
所成角的余弦值;
(2)求证: .
.
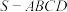 中,底面
中,底面 是正方形,平面
是正方形,平面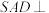 平面
平面 ,
,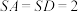 ,
,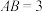 .
.
(1)求
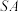 与
与 所成角的余弦值;
所成角的余弦值;(2)求证:
 .
.30.已知抛物线的顶点是坐标原点 ,焦点
,焦点 在
在 轴的正半轴上,
轴的正半轴上, 是抛物线上的点,点
是抛物线上的点,点 到焦点
到焦点 的距离为1,且到
的距离为1,且到 轴的距离是
轴的距离是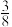 .
.
(1)求抛物线的标准方程;
(2)假设直线 通过点
通过点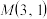 ,与抛物线相交于
,与抛物线相交于 ,
, 两点,且
两点,且 ,求直线
,求直线 的方程.
的方程.
 ,焦点
,焦点 在
在 轴的正半轴上,
轴的正半轴上, 是抛物线上的点,点
是抛物线上的点,点 到焦点
到焦点 的距离为1,且到
的距离为1,且到 轴的距离是
轴的距离是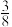 .
.(1)求抛物线的标准方程;
(2)假设直线
 通过点
通过点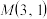 ,与抛物线相交于
,与抛物线相交于 ,
, 两点,且
两点,且 ,求直线
,求直线 的方程.
的方程. 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错
