全一卷
1.定义集合运算: .设
.设 .则集合
.则集合 的所有元素之和为( ).
的所有元素之和为( ).
 .设
.设 .则集合
.则集合 的所有元素之和为( ).
的所有元素之和为( ).| A.16 | B.18 | C.20 | D.22 |
2.已知 是等比数列,
是等比数列, .则
.则 (
( )的取值范围是( ).
)的取值范围是( ).
 是等比数列,
是等比数列, .则
.则 (
( )的取值范围是( ).
)的取值范围是( ).A. | B. | C. | D. |
3.5名志愿者随机进入三个不同的奥运场馆参加接待工作.则每个场馆至少有一名志愿者的概率为( ).
A.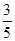 | B. | C. | D. |
4.已知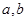 为非零的不共线的向量,设条件
为非零的不共线的向量,设条件 ;条件
;条件 :对一切
:对一切 ,不等式
,不等式 恒成立.则
恒成立.则 是
是 的( )
的( )
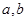 为非零的不共线的向量,设条件
为非零的不共线的向量,设条件 ;条件
;条件 :对一切
:对一切 ,不等式
,不等式 恒成立.则
恒成立.则 是
是 的( )
的( )| A.必要而不充分条件 | B.充分而不必要条件 |
| C.充分而且必要条件 | D.既不充分又不必要条件 |
5.设函数 定义在
定义在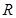 上,给出下述三个命题:
上,给出下述三个命题:
①满足条件 的函数图像关于点
的函数图像关于点 对称;
对称;
②满足条件 的函数图像关于直线
的函数图像关于直线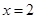 对称;
对称;
③函数 与
与 在同一坐标系中,其图像关于直线
在同一坐标系中,其图像关于直线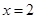 对称.
对称.
其中,真命题的个数是( )
 定义在
定义在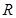 上,给出下述三个命题:
上,给出下述三个命题:①满足条件
 的函数图像关于点
的函数图像关于点 对称;
对称;②满足条件
 的函数图像关于直线
的函数图像关于直线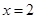 对称;
对称;③函数
 与
与 在同一坐标系中,其图像关于直线
在同一坐标系中,其图像关于直线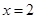 对称.
对称.其中,真命题的个数是( )
A. | B.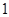 | C. | D. |
6.联结球面上两点的线段称为球的弦.半径为4的球的两条弦 的长度分别等于
的长度分别等于 分别为
分别为 的中点,每两条弦的两端都在球面上运动.给出下面四个命题:
的中点,每两条弦的两端都在球面上运动.给出下面四个命题:
①弦 可能交于点
可能交于点 ;②弦
;②弦 可能交于点
可能交于点 ;③
;③ 的最大值为5;④
的最大值为5;④ 的最小值为1.其中,真命题为( )
的最小值为1.其中,真命题为( )
 的长度分别等于
的长度分别等于 分别为
分别为 的中点,每两条弦的两端都在球面上运动.给出下面四个命题:
的中点,每两条弦的两端都在球面上运动.给出下面四个命题:①弦
 可能交于点
可能交于点 ;②弦
;②弦 可能交于点
可能交于点 ;③
;③ 的最大值为5;④
的最大值为5;④ 的最小值为1.其中,真命题为( )
的最小值为1.其中,真命题为( )| A.①③④ | B.①②③ | C.①②④ | D.②③④ |
7.设 .则
.则 的大小关系是( ).
的大小关系是( ).
 .则
.则 的大小关系是( ).
的大小关系是( ).A. | B. | C. | D. |
8.设函数 且
且 。则
。则 ( )
( )
 且
且 。则
。则 ( )
( )A. | B.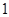 | C. | D.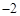 |
9.在平面直角坐标系中定义点 之间的交通距离为
之间的交通距离为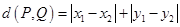 .
.
若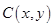 到点
到点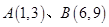 的交通距离相等,其中,实数
的交通距离相等,其中,实数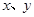 满足
满足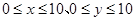 ,则所有满足条件的点
,则所有满足条件的点 的轨迹的长之和为____________.
的轨迹的长之和为____________.
 之间的交通距离为
之间的交通距离为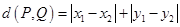 .
.若
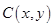 到点
到点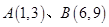 的交通距离相等,其中,实数
的交通距离相等,其中,实数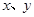 满足
满足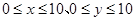 ,则所有满足条件的点
,则所有满足条件的点 的轨迹的长之和为____________.
的轨迹的长之和为____________.10.已知集合 .若点
.若点 满足
满足 且
且 ,则称点
,则称点 优于
优于 .如果集合
.如果集合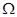 中的点
中的点 满足:不存在
满足:不存在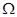 中的其他点优于
中的其他点优于 ,则所有这样的点
,则所有这样的点 构成的集合为______.
构成的集合为______.
 .若点
.若点 满足
满足 且
且 ,则称点
,则称点 优于
优于 .如果集合
.如果集合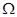 中的点
中的点 满足:不存在
满足:不存在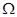 中的其他点优于
中的其他点优于 ,则所有这样的点
,则所有这样的点 构成的集合为______.
构成的集合为______.11.多项式 的展开式在合并同类项后,
的展开式在合并同类项后, 的系数为______(用数字作答).
的系数为______(用数字作答).
 的展开式在合并同类项后,
的展开式在合并同类项后, 的系数为______(用数字作答).
的系数为______(用数字作答).12.一个六棱柱的底面是正六边形,其侧棱垂直于底面.已知该六棱柱的顶点都在同一球面上,且该六棱柱的体积为 ,底面周长为3,则这个球的体积为
,底面周长为3,则这个球的体积为___________ .
 ,底面周长为3,则这个球的体积为
,底面周长为3,则这个球的体积为13.将一个 棋盘中的8个小方格染为黑色,使得每行、每列都恰有2个黑色方格则有______种不同的染法
棋盘中的8个小方格染为黑色,使得每行、每列都恰有2个黑色方格则有______种不同的染法
 棋盘中的8个小方格染为黑色,使得每行、每列都恰有2个黑色方格则有______种不同的染法
棋盘中的8个小方格染为黑色,使得每行、每列都恰有2个黑色方格则有______种不同的染法14.某校课外活动小组,在坐标纸上某沙漠设计植树方案如下:第 棵树种植在点
棵树种植在点 处,其中,
处,其中, .当
.当 时,
时, 其中,
其中, 表示实数
表示实数 的整数部分(如
的整数部分(如 .按此方案,第2008棵树种植点的坐标为______.
.按此方案,第2008棵树种植点的坐标为______.
 棵树种植在点
棵树种植在点 处,其中,
处,其中, .当
.当 时,
时, 其中,
其中, 表示实数
表示实数 的整数部分(如
的整数部分(如 .按此方案,第2008棵树种植点的坐标为______.
.按此方案,第2008棵树种植点的坐标为______.15.设实数 为正实数.求证:
为正实数.求证: ,当且仅当
,当且仅当 或
或 时,上式等号成立.
时,上式等号成立.
 为正实数.求证:
为正实数.求证: ,当且仅当
,当且仅当 或
或 时,上式等号成立.
时,上式等号成立.16.甲、乙两人进行乒乓球比赛,采用五局三胜制(即先胜三局者获冠军).对于每局比赛,甲获胜的概率为 ,乙获胜的概率为
,乙获胜的概率为 .若将“乙获得冠军”的事件称为“爆出冷门”试求该赛事爆出冷门的概率.
.若将“乙获得冠军”的事件称为“爆出冷门”试求该赛事爆出冷门的概率.
 ,乙获胜的概率为
,乙获胜的概率为 .若将“乙获得冠军”的事件称为“爆出冷门”试求该赛事爆出冷门的概率.
.若将“乙获得冠军”的事件称为“爆出冷门”试求该赛事爆出冷门的概率.17.已知函数 在区间
在区间 (
( )上的最小值为
)上的最小值为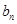 ,令
,令 (
( ).求证:
).求证: .
.
 在区间
在区间 (
( )上的最小值为
)上的最小值为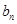 ,令
,令 (
( ).求证:
).求证: .
.18.过直线 上的点
上的点 作椭圆
作椭圆 的切线
的切线 ,切点分别为
,切点分别为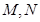 ,联结
,联结 .
.
(1)当点 在直线
在直线 上运动时,证明:直线
上运动时,证明:直线 恒过定点
恒过定点 ;
;
(2)当 时,定点
时,定点 平分线段
平分线段 .
.
 上的点
上的点 作椭圆
作椭圆 的切线
的切线 ,切点分别为
,切点分别为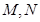 ,联结
,联结 .
.(1)当点
 在直线
在直线 上运动时,证明:直线
上运动时,证明:直线 恒过定点
恒过定点 ;
;(2)当
 时,定点
时,定点 平分线段
平分线段 .
. 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
