搜索
全一卷
难度系数：0.65 
答案解析
有奖纠错
1．设正六边形ABCDEF的边长为1，则
______ .
______ .2．双曲线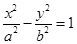
的右焦点为F，离心率为e，过点F且倾斜角为
的直线与该双曲线交于点A、B，若AB的中点为M，且|FM|等于半焦距，则
_____ .
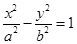的右焦点为F，离心率为e，过点F且倾斜角为
的直线与该双曲线交于点A、B，若AB的中点为M，且|FM|等于半焦距，则
_____ .3．满足(a+bi)6=a－bi(其中a，b∈R，i2=－1)的有序数组(a，b)的组数是_____ .
4．已知正四棱锥
的高为3，侧面与底面所成角为，先在内放入一个内切球O1，然后依次放入球
，使得后放入的各球均与前一个球及的四个侧面均相切，则放入所有球的体积之和为_____ .
的高为3，侧面与底面所成角为，先在内放入一个内切球O1，然后依次放入球
，使得后放入的各球均与前一个球及的四个侧面均相切，则放入所有球的体积之和为5．设一个袋子里有红、黄、蓝色小球各一个现每次从袋子里取出一个球(取出某色球的概率均相同)，确定颜色后放回，直到连续两次均取出红色球时为止，记此时取出球的次数为ξ，则ξ的数学期望为_____ .
6．已知a为实数，且对任意k∈[－1，1]当x∈(0，6]时，6lnx+x2－8x+a≤kx恒成立，则a的最大值是_____ .
7．已知数列{an}满足：
，其中[x]表示不超过实数x的最大整数.设C为实数，且对任意的正整数n，都有
，则C的最小值是_____ .
，其中[x]表示不超过实数x的最大整数.设C为实数，且对任意的正整数n，都有
，则C的最小值是_____ .8．若正整数n使得方程
有正整数解(x，y，z)，称n为“好数”.则不超过2019的“好数”个数是_____ .
有正整数解(x，y，z)，称n为“好数”.则不超过2019的“好数”个数是_____ .9．设点A的坐标为(0，3)，点B、C为圆
上的两动点，满足∠BAC=90°，求△ABC面积的最大值.
上的两动点，满足∠BAC=90°，求△ABC面积的最大值.10．设a，b，c∈(0，1]，
为实数，使得
恒成立，求的最大值.
为实数，使得
恒成立，求的最大值.11．已知函数f(x)=xlnx－ax2，a∈R.
（1）证明：当1<x<3时，
；
（2）设函数F(x)=|f(x)|(x∈[1，e])有极小值，求a的取值范围.
（1）证明：当1<x<3时，
；（2）设函数F(x)=|f(x)|(x∈[1，e])有极小值，求a的取值范围.
