全一卷
1.若函数 ,且
,且 .则
.则
 ______.
______.
 ,且
,且 .则
.则
 ______.
______.2.已知直线 和圆
和圆 ,点
,点 在直线
在直线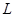 上,
上, ,
, 为圆
为圆 上两点,在
上两点,在 中,
中, ,
, 过圆心
过圆心 ,则点
,则点 横坐标范围为
横坐标范围为___________ .
 和圆
和圆 ,点
,点 在直线
在直线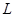 上,
上, ,
, 为圆
为圆 上两点,在
上两点,在 中,
中, ,
, 过圆心
过圆心 ,则点
,则点 横坐标范围为
横坐标范围为3.在坐标平面上有两个区域 和
和 ,
, 为
为 ,
, 是随
是随 变化的区域,它由不等式
变化的区域,它由不等式 所确定,
所确定, 的取值范围是
的取值范围是 ,则
,则 和
和 的公共面积是函数
的公共面积是函数 .
.
 和
和 ,
, 为
为 ,
, 是随
是随 变化的区域,它由不等式
变化的区域,它由不等式 所确定,
所确定, 的取值范围是
的取值范围是 ,则
,则 和
和 的公共面积是函数
的公共面积是函数 .
.
4.使不等式 对一切正整数
对一切正整数 都成立的最小正整数
都成立的最小正整数 的值为
的值为____ .
 对一切正整数
对一切正整数 都成立的最小正整数
都成立的最小正整数 的值为
的值为5.椭圆
 上任意两点
上任意两点 ,
, ,若
,若 ,则乘积
,则乘积 的最小值为 .
的最小值为 .

 上任意两点
上任意两点 ,
, ,若
,若 ,则乘积
,则乘积 的最小值为 .
的最小值为 .6.若方程 仅有一个实根,那么
仅有一个实根,那么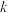 的取值范围是
的取值范围是_________ .
 仅有一个实根,那么
仅有一个实根,那么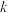 的取值范围是
的取值范围是7.一个由若干行数字组成的数表,从第二行起每一行中的数字均等于其肩上的两个数之和,最后一行仅有一个数,第一行是前100个正整数按从小到大排成的行.则最后一行的数是______ (可以用指数表示).
8.某车站每天早上8:00~9:00、9:00~10:00都恰有一辆客车到站,但到站的时刻是随机的,且两者到站的时间是相互独立的,其规律见表1.一旅客8:20到站.则他候车时间的数学期望为______(精确到分).
表1
表1
| 到站时刻 | 8:10~9:10 | 8:30~9:30 | 8:50~9:50 |
| 概率 |  | 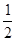 |  |
9. 设直线 (其中
(其中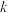 ,
, 为整数)与椭圆
为整数)与椭圆 交于不同两点
交于不同两点 ,
, ,与双曲线
,与双曲线 交于不同两点
交于不同两点 ,
, ,问是否存在直线
,问是否存在直线 ,使得向量
,使得向量 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由.
 (其中
(其中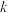 ,
, 为整数)与椭圆
为整数)与椭圆 交于不同两点
交于不同两点 ,
, ,与双曲线
,与双曲线 交于不同两点
交于不同两点 ,
, ,问是否存在直线
,问是否存在直线 ,使得向量
,使得向量 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由.10.已知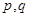 (
( 是实数,方程
是实数,方程 有两个实根
有两个实根 ,数列
,数列 满足
满足 (
( ).
).
(1)求数列 的通项公式(用
的通项公式(用 表示);
表示);
(2)若 ,求
,求 的前
的前 项和.
项和.
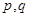 (
( 是实数,方程
是实数,方程 有两个实根
有两个实根 ,数列
,数列 满足
满足 (
( ).
).(1)求数列
 的通项公式(用
的通项公式(用 表示);
表示);(2)若
 ,求
,求 的前
的前 项和.
项和.11.求函数 的最大值和最小值.
的最大值和最小值.
 的最大值和最小值.
的最大值和最小值.12.如图, 分别为锐角
分别为锐角 (
( )的外接圆圆
)的外接圆圆 上弧
上弧 的中点.过点
的中点.过点 作
作 交圆
交圆 于点
于点 为
为 的内心,联结
的内心,联结 并延长交圆
并延长交圆 于点
于点 ,
,
求证:(1) ;
;
(2)在弧 (不含点
(不含点 )上任取一点
)上任取一点 (
( ),记
),记 的内心分别
的内心分别 ,则
,则 四点共圆.
四点共圆.
 分别为锐角
分别为锐角 (
( )的外接圆圆
)的外接圆圆 上弧
上弧 的中点.过点
的中点.过点 作
作 交圆
交圆 于点
于点 为
为 的内心,联结
的内心,联结 并延长交圆
并延长交圆 于点
于点 ,
,求证:(1)
 ;
;(2)在弧
 (不含点
(不含点 )上任取一点
)上任取一点 (
( ),记
),记 的内心分别
的内心分别 ,则
,则 四点共圆.
四点共圆.
13.求证:不等式 (
( )
)
 (
( )
)14.设 是给定的两个正整数.证明:有无穷多个正整数
是给定的两个正整数.证明:有无穷多个正整数 (
( ),使得
),使得 与
与 互质.
互质.
 是给定的两个正整数.证明:有无穷多个正整数
是给定的两个正整数.证明:有无穷多个正整数 (
( ),使得
),使得 与
与 互质.
互质.15.在非负数构成的 数表
数表 中,每行的数互不相同,前六列中每列的三数之和为1,
中,每行的数互不相同,前六列中每列的三数之和为1, 均大于1.如果
均大于1.如果 的前三列构成的数表
的前三列构成的数表 满足下面的性质
满足下面的性质 :对于数表
:对于数表 中的任意一列
中的任意一列 (
( )均存在某个
)均存在某个 使得
使得 .①
.①
求证:(1)最小值 (
( )一定去自数表
)一定去自数表 的不同列;
的不同列;
(2)存在数表 中唯一的一列
中唯一的一列 (
( )使得
)使得 数表
数表 仍然具有性质(
仍然具有性质( ).
).
 数表
数表 中,每行的数互不相同,前六列中每列的三数之和为1,
中,每行的数互不相同,前六列中每列的三数之和为1, 均大于1.如果
均大于1.如果 的前三列构成的数表
的前三列构成的数表 满足下面的性质
满足下面的性质 :对于数表
:对于数表 中的任意一列
中的任意一列 (
( )均存在某个
)均存在某个 使得
使得 .①
.①求证:(1)最小值
 (
( )一定去自数表
)一定去自数表 的不同列;
的不同列;(2)存在数表
 中唯一的一列
中唯一的一列 (
( )使得
)使得 数表
数表 仍然具有性质(
仍然具有性质( ).
). 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
