全一卷
1.已知集合 ,
, ,则
,则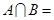 ( )
( )
 ,
, ,则
,则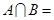 ( )
( )A. | B. | C. | D. |
2.已知复数 (i是虚数单位),则
(i是虚数单位),则 ( )
( )
 (i是虚数单位),则
(i是虚数单位),则 ( )
( )| A.1 | B.2 | C. | D.3 |
3.函数 的最小正周期是( )
的最小正周期是( )
 的最小正周期是( )
的最小正周期是( )A. | B.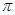 | C. | D. |
4.已知 为定义在R上的奇函数,且
为定义在R上的奇函数,且 ,下列一定在函数
,下列一定在函数 图象上的点是( )
图象上的点是( )
 为定义在R上的奇函数,且
为定义在R上的奇函数,且 ,下列一定在函数
,下列一定在函数 图象上的点是( )
图象上的点是( )A. | B. | C. | D. |
5.已知a,3,b,9,c成等比数列,且 ,则
,则 等于( )
等于( )
 ,则
,则 等于( )
等于( )A. | B.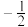 | C. | D.1 |
6.已知抛物线 (
( )的焦点与双曲线
)的焦点与双曲线 的右焦点重合,则
的右焦点重合,则 ( )
( )
 (
( )的焦点与双曲线
)的焦点与双曲线 的右焦点重合,则
的右焦点重合,则 ( )
( )A. | B.2 | C.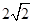 | D.4 |
7.在 的展开式中,常数项是( )
的展开式中,常数项是( )
 的展开式中,常数项是( )
的展开式中,常数项是( )A. | B. | C.20 | D.160 |
8.在平面直角坐标系中,O为坐标原点,已知两点 ,
, .则
.则 ( )
( )
 ,
, .则
.则 ( )
( )| A.1 | B. | C.2 | D.与 有关 有关 |
9.若 ,
, ,则“
,则“ ”是“
”是“ ”的( )
”的( )
 ,
, ,则“
,则“ ”是“
”是“ ”的( )
”的( )| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
10.某同学在数学探究活动中确定研究主题是“ (
( ,
, )是几位数”,他以
)是几位数”,他以 (
( )为例做研究,得出相应的结论,其研究过程及部分研究数据如表:
)为例做研究,得出相应的结论,其研究过程及部分研究数据如表:
试用该同学的研究结论判断 是几位数(参考数据
是几位数(参考数据 ,
, )( )
)( )
 (
( ,
, )是几位数”,他以
)是几位数”,他以 (
( )为例做研究,得出相应的结论,其研究过程及部分研究数据如表:
)为例做研究,得出相应的结论,其研究过程及部分研究数据如表: ( ( ) ) |  | N的位数 |
 |  | 一位数 |
 |  | 一位数 |
 |  | 一位数 |
 |  | 两位数 |
 |  | 两位数 |
 |  | 两位数 |
 |  | 三位数 |
 |  | 三位数 |
 |  | 三位数 |
 |  | 四位数 |
| …… | …… | …… |
试用该同学的研究结论判断
 是几位数(参考数据
是几位数(参考数据 ,
, )( )
)( )| A.101 | B.50 | C.31 | D.30 |
11.已知向量 ,
, ,其中
,其中 .若
.若 ,
, 共线,则m等于______.
共线,则m等于______.
 ,
, ,其中
,其中 .若
.若 ,
, 共线,则m等于______.
共线,则m等于______.12.圆 的圆心到直线
的圆心到直线 的距离为______.
的距离为______.
 的圆心到直线
的圆心到直线 的距离为______.
的距离为______.13.某三棱锥的三视图如图所示,则该三棱锥的体积等于______.

14.给出下列四个函数,① ;②
;② ;③
;③ ;④
;④ ,其中值域为
,其中值域为 的函数的序号是______.
的函数的序号是______.
 ;②
;② ;③
;③ ;④
;④ ,其中值域为
,其中值域为 的函数的序号是______.
的函数的序号是______.15.中国古代数学著作《孙子算经》中有这样一道算术题:“今有物不知其数,三三数之余二,五五数之余三,问物几何?”,将上述问题的所有正整数答案从小到大组成一个数列 ,则
,则
______ ;
______ .(注:三三数之余二是指此数被3除余2,例如“5”)
 ,则
,则

16.已知 ,满足
,满足 ,
, ,______,判断
,______,判断 的面积
的面积 是否成立?说明理由.
是否成立?说明理由.
从① ;②
;② 这两个条件中任选一个,补充到上面问题条件中的空格处并作答.
这两个条件中任选一个,补充到上面问题条件中的空格处并作答.
注:如果选择多个条件分别解答,按第一个解答计分.
 ,满足
,满足 ,
, ,______,判断
,______,判断 的面积
的面积 是否成立?说明理由.
是否成立?说明理由.从①
 ;②
;② 这两个条件中任选一个,补充到上面问题条件中的空格处并作答.
这两个条件中任选一个,补充到上面问题条件中的空格处并作答.注:如果选择多个条件分别解答,按第一个解答计分.
17. 年
年 月
月 日,我国开始施行《个人所得税专项附加扣除操作办法》,附加扣除的专项包括子女教育、继续教育、大病医疗、住房贷款利息、住房租金、赡养老人.某单位有老年员工
日,我国开始施行《个人所得税专项附加扣除操作办法》,附加扣除的专项包括子女教育、继续教育、大病医疗、住房贷款利息、住房租金、赡养老人.某单位有老年员工 人,中年员工
人,中年员工 人,青年员工
人,青年员工 人,现采用分层抽样的方法,从该单位员工中抽取
人,现采用分层抽样的方法,从该单位员工中抽取 人,调查享受个人所得税专项附加扣除的情况,并按照员工类别进行各专项人数汇总,数据统计如表:
人,调查享受个人所得税专项附加扣除的情况,并按照员工类别进行各专项人数汇总,数据统计如表:
(Ⅰ)在抽取的 人中,老年员工、中年员工、青年员工各有多少人;
人中,老年员工、中年员工、青年员工各有多少人;
(Ⅱ)从上表享受住房贷款利息专项扣除的员工中随机选取 人,记
人,记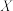 为选出的中年员工的人数,求
为选出的中年员工的人数,求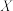 的分布列和数学期望.
的分布列和数学期望.
 年
年 月
月 日,我国开始施行《个人所得税专项附加扣除操作办法》,附加扣除的专项包括子女教育、继续教育、大病医疗、住房贷款利息、住房租金、赡养老人.某单位有老年员工
日,我国开始施行《个人所得税专项附加扣除操作办法》,附加扣除的专项包括子女教育、继续教育、大病医疗、住房贷款利息、住房租金、赡养老人.某单位有老年员工 人,中年员工
人,中年员工 人,青年员工
人,青年员工 人,现采用分层抽样的方法,从该单位员工中抽取
人,现采用分层抽样的方法,从该单位员工中抽取 人,调查享受个人所得税专项附加扣除的情况,并按照员工类别进行各专项人数汇总,数据统计如表:
人,调查享受个人所得税专项附加扣除的情况,并按照员工类别进行各专项人数汇总,数据统计如表:专项员工人数 | 子女教育 | 继续教育 | 大病医疗 | 住房贷款利息 | 住房租金 | 赡养老人 |
老员工 |
|
|
|
|
|
|
中年员工 |
|
|
|
|
|
|
青年员工 |
|
|
|
|
|
|
(Ⅰ)在抽取的
 人中,老年员工、中年员工、青年员工各有多少人;
人中,老年员工、中年员工、青年员工各有多少人;(Ⅱ)从上表享受住房贷款利息专项扣除的员工中随机选取
 人,记
人,记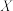 为选出的中年员工的人数,求
为选出的中年员工的人数,求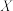 的分布列和数学期望.
的分布列和数学期望.18.如图,已知四边形 为菱形,且
为菱形,且 ,取
,取 中点为
中点为 .现将四边形
.现将四边形 沿
沿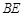 折起至
折起至 ,使得
,使得 .
.

(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求二面角 的余弦值;
的余弦值;
(Ⅲ)若点 满足
满足 ,当
,当 平面
平面 时,求
时,求 的值.
的值.
 为菱形,且
为菱形,且 ,取
,取 中点为
中点为 .现将四边形
.现将四边形 沿
沿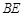 折起至
折起至 ,使得
,使得 .
.
(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)求二面角
 的余弦值;
的余弦值;(Ⅲ)若点
 满足
满足 ,当
,当 平面
平面 时,求
时,求 的值.
的值.19.已知椭圆 的离心率为
的离心率为 ,点
,点 在椭圆
在椭圆 上.
上.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设 为原点,过原点的直线(不与
为原点,过原点的直线(不与 轴垂直)与椭圆
轴垂直)与椭圆 交于
交于 、
、 两点,直线
两点,直线 、
、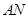 与
与 轴分别交于点
轴分别交于点 、
、 .问:
.问: 轴上是否存在定点
轴上是否存在定点 ,使得
,使得 ?若存在,求点
?若存在,求点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
 的离心率为
的离心率为 ,点
,点 在椭圆
在椭圆 上.
上.(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)设
 为原点,过原点的直线(不与
为原点,过原点的直线(不与 轴垂直)与椭圆
轴垂直)与椭圆 交于
交于 、
、 两点,直线
两点,直线 、
、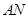 与
与 轴分别交于点
轴分别交于点 、
、 .问:
.问: 轴上是否存在定点
轴上是否存在定点 ,使得
,使得 ?若存在,求点
?若存在,求点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.20.已知函数 ,设
,设 .
.
(Ⅰ)求 的极小值;
的极小值;
(Ⅱ)若 在
在 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.
 ,设
,设 .
. (Ⅰ)求
 的极小值;
的极小值;(Ⅱ)若
 在
在 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.21.用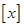 表示一个小于或等于
表示一个小于或等于 的最大整数.如:
的最大整数.如: ,
, ,
, . 已知实数列
. 已知实数列 、
、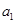 、
、 对于所有非负整数
对于所有非负整数 满足
满足 ,其中
,其中 是任意一个非零实数.
是任意一个非零实数.
(Ⅰ)若 ,写出
,写出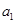 、
、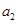 、
、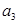 ;
;
(Ⅱ)若 ,求数列
,求数列 的最小值;
的最小值;
(Ⅲ)证明:存在非负整数 ,使得当
,使得当 时,
时, .
.
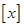 表示一个小于或等于
表示一个小于或等于 的最大整数.如:
的最大整数.如: ,
, ,
, . 已知实数列
. 已知实数列 、
、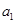 、
、 对于所有非负整数
对于所有非负整数 满足
满足 ,其中
,其中 是任意一个非零实数.
是任意一个非零实数.(Ⅰ)若
 ,写出
,写出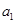 、
、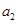 、
、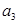 ;
;(Ⅱ)若
 ,求数列
,求数列 的最小值;
的最小值;(Ⅲ)证明:存在非负整数
 ,使得当
,使得当 时,
时, .
. 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错