全一卷
1.已知yz≠0,且集合{2x,3z,xy}也可以表示为{y,2x2,3xz},则x=____________.
2.如果函数 的图象关于点
的图象关于点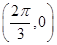 中心对称,那么
中心对称,那么 的最小值为____________ .
的最小值为____________ .
 的图象关于点
的图象关于点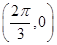 中心对称,那么
中心对称,那么 的最小值为____________ .
的最小值为____________ .3.设函数 ,则y的最小值为____________ .
,则y的最小值为____________ .
 ,则y的最小值为____________ .
,则y的最小值为____________ .4.已知点P(-2,5)在圆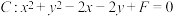 上,直线l:
上,直线l: 与圆C相交于A、B两点,则
与圆C相交于A、B两点,则
____________ .
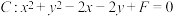 上,直线l:
上,直线l: 与圆C相交于A、B两点,则
与圆C相交于A、B两点,则
5.已知xyz+y+z=12,则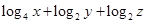 的最大值为____________ .
的最大值为____________ .
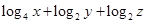 的最大值为____________ .
的最大值为____________ .6.从1,2,…,20中任取3个不同的数,这3个数构成等差数列的概率为____________ .
7.棱长为6的正方体内有一个棱长为x的正四面体,且该四面体可以在正方体内任意转动,则x的最大值为____________ .
8.满足 的正整数对(x,y)有____________ 对.
的正整数对(x,y)有____________ 对.
 的正整数对(x,y)有____________ 对.
的正整数对(x,y)有____________ 对.9.已知函数 .
.
(1)设a>1,讨论f(x)在区间(0,1)上的单调性;
(2)设a>0,求f(x)的极值.
 .
.(1)设a>1,讨论f(x)在区间(0,1)上的单调性;
(2)设a>0,求f(x)的极值.
10.设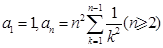 .求证:
.求证:
(1)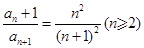 ;
;
(2)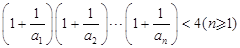 .
.
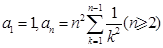 .求证:
.求证:(1)
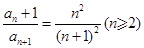 ;
;(2)
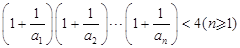 .
.11.如图所示,AD、AH分别是△ABC(其中AB>AC)的角平分线、高线,点M是AD的中点,△MDH的外接圆交CM于点E.求证:∠AEB=90°.

12.如图所示,设k>0且k≠1,直线l:y=kx+1与l1:y=k1x+1关于直线y=x+1对称,直线l与l1分别交椭圆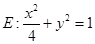 于点A、M和A、N.
于点A、M和A、N.

(1)求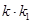 的值;
的值;
(2)求证:对任意的实数k,直线MN恒过定点.
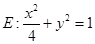 于点A、M和A、N.
于点A、M和A、N.
(1)求
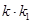 的值;
的值;(2)求证:对任意的实数k,直线MN恒过定点.
 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
