全一卷
1.已知集合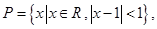
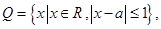 且
且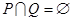 .则实数
.则实数 取值范围为.
取值范围为.
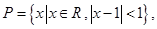
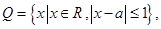 且
且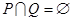 .则实数
.则实数 取值范围为.
取值范围为.A.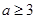 | B. | C. 或 或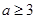 | D. |
2.若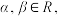 则
则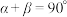 是
是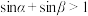 的
的
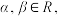 则
则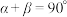 是
是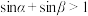 的
的| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
3.已知等比数列{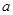
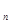 }:
}: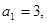 且第一项至第八项的几何平均数为9,则第三项是( )
且第一项至第八项的几何平均数为9,则第三项是( )
 }:
}: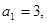 且第一项至第八项的几何平均数为9,则第三项是( )
且第一项至第八项的几何平均数为9,则第三项是( )A. | B. | C. | D. |
4.已知复数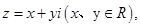 且
且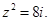 则
则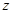 =( ).
=( ).
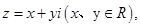 且
且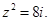 则
则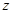 =( ).
=( ).| A.2+2i | B.-2+2i或2-2i | C.-2-2i | D.2+2i或-2-2i |
5.已知直线 与抛物线
与抛物线 交于
交于 两点,
两点,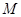 为
为 的中点,
的中点, 为抛物线上一个动点,若
为抛物线上一个动点,若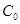 满足
满足 ,则下列一定成立的是( )。
,则下列一定成立的是( )。
 与抛物线
与抛物线 交于
交于 两点,
两点,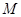 为
为 的中点,
的中点, 为抛物线上一个动点,若
为抛物线上一个动点,若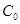 满足
满足 ,则下列一定成立的是( )。
,则下列一定成立的是( )。A. | B. 其中 其中 是抛物线过 是抛物线过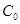 的切线 的切线 |
C. | D. |
6.若三位数 被7整除,且
被7整除,且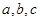 成公差非零的等差数列,则这样的整数共有( )个。
成公差非零的等差数列,则这样的整数共有( )个。
 被7整除,且
被7整除,且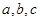 成公差非零的等差数列,则这样的整数共有( )个。
成公差非零的等差数列,则这样的整数共有( )个。| A.4 | B.6 | C.7 | D.8 |
7.某程序框图如下,当E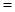 0.96时,则输出的K=( )
0.96时,则输出的K=( )
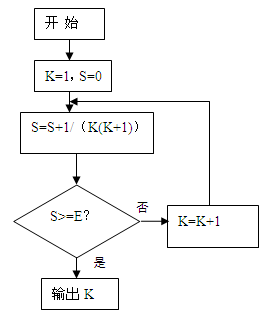
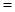 0.96时,则输出的K=( )
0.96时,则输出的K=( )
| A.20 | B.22 | C.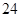 | D.25 |
8.已知一个立体图形的三视图如图所示,则该立体图形的体积为( ) .
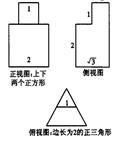

A. | B. | C. | D. |
9.设函数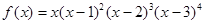 ,则函数
,则函数 的极大值点为( )
的极大值点为( )
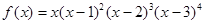 ,则函数
,则函数 的极大值点为( )
的极大值点为( )A. | B. | C.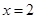 | D.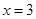 |
10.已知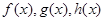 为一次函数,若对实数
为一次函数,若对实数 满足
满足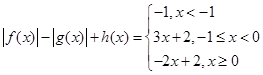 ,
,
则 的表达式为( )。
的表达式为( )。
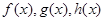 为一次函数,若对实数
为一次函数,若对实数 满足
满足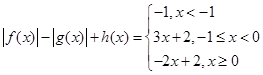 ,
,则
 的表达式为( )。
的表达式为( )。A. |
B. |
C. |
D. |
11.若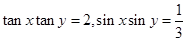 ,则
,则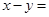
_________________ .
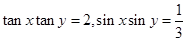 ,则
,则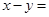
12.已知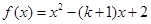 ,若当
,若当 时
时 恒大于零,则
恒大于零,则 的取值范围为
的取值范围为_____________ .
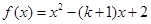 ,若当
,若当 时
时 恒大于零,则
恒大于零,则 的取值范围为
的取值范围为13.数列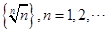 ,则数列中最大项的值为
,则数列中最大项的值为______________ .
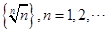 ,则数列中最大项的值为
,则数列中最大项的值为14.若x、y∈R满足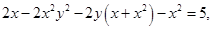 则
则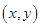 =_______.
=_______.
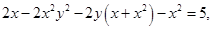 则
则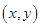 =_______.
=_______.15.设直线 与曲线
与曲线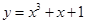 有三个不同的交点
有三个不同的交点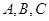 ,且
,且 ,则直线
,则直线 的方程为
的方程为_________________ .
 与曲线
与曲线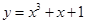 有三个不同的交点
有三个不同的交点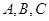 ,且
,且 ,则直线
,则直线 的方程为
的方程为16.若 则
则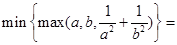
________________________ .
 则
则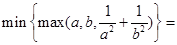
17.某动点在平 面直角坐标系 第一 象限的整点上运动 (含第一象限x轴、y轴上的整点),其运动规律为 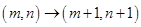 或
或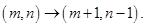 若该动点从原点出发,经过 6步运动到点
若该动点从原点出发,经过 6步运动到点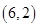 ,则有
,则有_______ 中不同的运动轨迹.
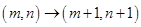 或
或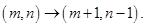 若该动点从原点出发,经过 6步运动到点
若该动点从原点出发,经过 6步运动到点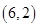 ,则有
,则有18.已知抛物线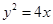 ,过x轴上点K的直线与抛物线交于点P、Q.证明:存在 唯一 一点K,使得
,过x轴上点K的直线与抛物线交于点P、Q.证明:存在 唯一 一点K,使得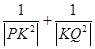 为常数,并确定点K的坐标。
为常数,并确定点K的坐标。
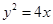 ,过x轴上点K的直线与抛物线交于点P、Q.证明:存在 唯一 一点K,使得
,过x轴上点K的直线与抛物线交于点P、Q.证明:存在 唯一 一点K,使得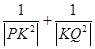 为常数,并确定点K的坐标。
为常数,并确定点K的坐标。19.设二次函数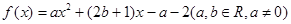 在[3,4]上至少有一个零点,求
在[3,4]上至少有一个零点,求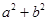 的最小值。
的最小值。
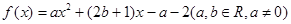 在[3,4]上至少有一个零点,求
在[3,4]上至少有一个零点,求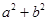 的最小值。
的最小值。20.设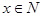 满足
满足 数列
数列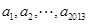 是公差为
是公差为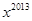 ,首项
,首项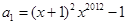 的等差数列; 数列
的等差数列; 数列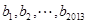 是公比为
是公比为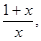 首项
首项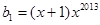 的等比数列,求证:
的等比数列,求证: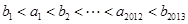 。
。
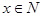 满足
满足 数列
数列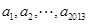 是公差为
是公差为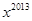 ,首项
,首项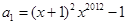 的等差数列; 数列
的等差数列; 数列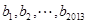 是公比为
是公比为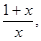 首项
首项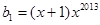 的等比数列,求证:
的等比数列,求证: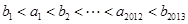 。
。21.设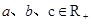 ,满足
,满足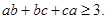 证明:
证明: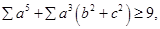 其中,“
其中,“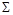 ” 表示轮换对称和.
” 表示轮换对称和.
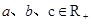 ,满足
,满足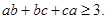 证明:
证明: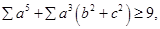 其中,“
其中,“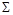 ” 表示轮换对称和.
” 表示轮换对称和.22.从0,1,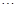 ,10中挑选若干个不 同的数字填满图中每一个 圆圈称为一种“填法”,若各条线段相连的两个圆 圈 内 的数字之差的绝对值各不相同 则称这样的填法为“完美填法”.问:图1和图2是否存在完美填法?若存在,请给出一种完美填法; 若不存在,请说明理由.
,10中挑选若干个不 同的数字填满图中每一个 圆圈称为一种“填法”,若各条线段相连的两个圆 圈 内 的数字之差的绝对值各不相同 则称这样的填法为“完美填法”.问:图1和图2是否存在完美填法?若存在,请给出一种完美填法; 若不存在,请说明理由.
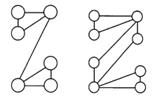
图1 图2
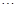 ,10中挑选若干个不 同的数字填满图中每一个 圆圈称为一种“填法”,若各条线段相连的两个圆 圈 内 的数字之差的绝对值各不相同 则称这样的填法为“完美填法”.问:图1和图2是否存在完美填法?若存在,请给出一种完美填法; 若不存在,请说明理由.
,10中挑选若干个不 同的数字填满图中每一个 圆圈称为一种“填法”,若各条线段相连的两个圆 圈 内 的数字之差的绝对值各不相同 则称这样的填法为“完美填法”.问:图1和图2是否存在完美填法?若存在,请给出一种完美填法; 若不存在,请说明理由.
图1 图2
 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错
