搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．设
.求
的值为.
.求
的值为.A． | B． | C． | D． |
2．若
，则
的取值范围是.
，则
的取值范围是.A． | B． | C． | D． |
3．设
.上述函数中，周期函数的个数是.
.上述函数中，周期函数的个数是.| A．1 | B．2 | C．3 | D．4 |
4．正方体的截面不可能是
①钝角三角形；②直角三角形；③菱形；④正五边形；⑤正六边形.
①钝角三角形；②直角三角形；③菱形；④正五边形；⑤正六边形.
| A．①②⑤ | B．①②④ | C．②③④ | D．③④⑤ |
5．已知a，b是两个相互垂直的单位向量，而
则对于任意实数
，
的最小值是.
则对于任意实数
，
的最小值是.| A．5 | B．7 | C．12 | D．13 |
6．设函数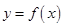
满足
.则方程
根的个数可能是.
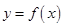满足
.则方程
根的个数可能是.| A．无穷多 | B．没有或者有限个 | C．有限个 | D．没有或者无穷多 |
7．设
求
________.
求
________.8．已知数列
，满足
，且
.则
_________.
，满足
，且
.则
_________.9．设函数
_________.
_________.10．设命题
和命题
对任何
有且仅有一个成立.则实数c的取值范围是_________.
和命题
对任何
有且仅有一个成立.则实数c的取值范围是_________.11．在x轴的正方向上，从左向右依次取点列
以及在第一象限内的抛物线
上从左向右依次取点列
使
都是等边三角形，其中
是坐标原点.则第2005个等边三角形的边长是__________.
以及在第一象限内的抛物线
上从左向右依次取点列
使
都是等边三角形，其中
是坐标原点.则第2005个等边三角形的边长是__________.12．根据指令，机器人在平面上能完成下列动作：如图，先从原点O沿正东偏北
方向行走一段时间后，再向正北方向行走一段时间，但何时改变方向不定.假定机器人行走速度为10m/min，则机器人行走2min时的可能落点区域的面积是__________.
方向行走一段时间后，再向正北方向行走一段时间，但何时改变方向不定.假定机器人行走速度为10m/min，则机器人行走2min时的可能落点区域的面积是__________.
13．设双曲线
的左、右焦点分别为
，若
的顶点P在第一象限的双曲线上移动，求的内切圆的圆心轨迹以及该内切圆在边
上的切点轨迹.
的左、右焦点分别为
，若
的顶点P在第一象限的双曲线上移动，求的内切圆的圆心轨迹以及该内切圆在边
上的切点轨迹.14．设
，定义
.
①求
的最小值；
②在
条件下，求的最小值；
③在
条件下，求的最小值，并加以证明.
，定义
.①求
的最小值；②在
条件下，求的最小值；③在
条件下，求的最小值，并加以证明.15．在一次实战军事演习中，红方的一条直线防线上设有20个岗位.为了试验5种不同的新式武器，打算安排5个岗位配备这些新式武器，要求第一个和最后一个岗位不配备新式武器，且每相邻5个岗位至少有一个岗位配备新式武器，相邻2个岗位不同时配备新式武器.问共有多少种配备新式武器的方案?
