全一卷
1.方程组 的解集是_______.
的解集是_______.
 的解集是_______.
的解集是_______.2.在平面直角坐标系中,长度为1的线段AB在 轴上移动(点A在B的左边),点P(0,1)与A连成直线,点Q(1,2)与B连成直线.则直线PA与QB的交点R的轨迹方程是
轴上移动(点A在B的左边),点P(0,1)与A连成直线,点Q(1,2)与B连成直线.则直线PA与QB的交点R的轨迹方程是________ .
 轴上移动(点A在B的左边),点P(0,1)与A连成直线,点Q(1,2)与B连成直线.则直线PA与QB的交点R的轨迹方程是
轴上移动(点A在B的左边),点P(0,1)与A连成直线,点Q(1,2)与B连成直线.则直线PA与QB的交点R的轨迹方程是3.已知M是椭圆 在第一象限的弧上一动点,MN ⊥y轴,垂足为N. 当△OMN面积最大时 ,其内切圆半径r=________.
在第一象限的弧上一动点,MN ⊥y轴,垂足为N. 当△OMN面积最大时 ,其内切圆半径r=________.
 在第一象限的弧上一动点,MN ⊥y轴,垂足为N. 当△OMN面积最大时 ,其内切圆半径r=________.
在第一象限的弧上一动点,MN ⊥y轴,垂足为N. 当△OMN面积最大时 ,其内切圆半径r=________.4.已知△ABC的外接圆半径为1,∠A、∠B、∠C的平分线分别交△ABC的外接圆于点 A1、B1、C1.则 _________.
_________.
 _________.
_________.5.设 ,其中,
,其中, 、b为实常数.若
、b为实常数.若 ,则
,则 _______.
_______.
 ,其中,
,其中, 、b为实常数.若
、b为实常数.若 ,则
,则 _______.
_______.6.在平面直角坐标系中,0为坐标原点,点A(3, )、B(3,b)使∠AOB=
)、B(3,b)使∠AOB=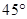 ,其中,
,其中, 、b均为整数,且
、b均为整数,且 b.则满足条件的数对(
b.则满足条件的数对( ,b)共有______ 组.
,b)共有______ 组.
 )、B(3,b)使∠AOB=
)、B(3,b)使∠AOB=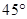 ,其中,
,其中, 、b均为整数,且
、b均为整数,且 b.则满足条件的数对(
b.则满足条件的数对( ,b)共有______ 组.
,b)共有______ 组.7.已知 C的方程为
C的方程为 ,直线
,直线 与
与 C交于A、B两点.则直线 AC、BC的倾斜角之和为_______.
C交于A、B两点.则直线 AC、BC的倾斜角之和为_______.
 C的方程为
C的方程为 ,直线
,直线 与
与 C交于A、B两点.则直线 AC、BC的倾斜角之和为_______.
C交于A、B两点.则直线 AC、BC的倾斜角之和为_______.8.甲、乙两运动员乒乓球比赛正在进行中,甲必须再胜2局才最后获胜;乙必须再胜3局才最后获胜,若甲、乙两人每局取胜的概率都是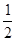 ,则甲最后获胜的概率是_____(用最简分数作答 ).
,则甲最后获胜的概率是_____(用最简分数作答 ).
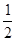 ,则甲最后获胜的概率是_____(用最简分数作答 ).
,则甲最后获胜的概率是_____(用最简分数作答 ).9.对于两个实数  、b,
、b, 表示
表示  、b中的较小数.求所有的非零实数
、b中的较小数.求所有的非零实数 ,使
,使
 、b,
、b, 表示
表示  、b中的较小数.求所有的非零实数
、b中的较小数.求所有的非零实数 ,使
,使
10.如图,在△ABC中,0为边BC的中点,点M、N分别在边AB、AC上,且AM=6,MB =4,AN=4,NC=3,∠MON=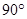 ,求∠A的大小.
,求∠A的大小.
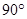 ,求∠A的大小.
,求∠A的大小.
11.对整数 k,定义集合 问:在 S0,S1,…S599这 600个集合中,有多少个集合不含有完全平方数?
问:在 S0,S1,…S599这 600个集合中,有多少个集合不含有完全平方数?
 问:在 S0,S1,…S599这 600个集合中,有多少个集合不含有完全平方数?
问:在 S0,S1,…S599这 600个集合中,有多少个集合不含有完全平方数?12.求所有大于l的正整数n,使得对任意正实数x1,x2,…,xn,都有不等式

 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
