全一卷
1.若正数a,b满足2+log2a=3+log3b=log6(a+b),则 的值为
的值为______________ .
 的值为
的值为2.设集合 中的最大、最小元素分别为M、m,则
中的最大、最小元素分别为M、m,则 的值为
的值为___________ .
 中的最大、最小元素分别为M、m,则
中的最大、最小元素分别为M、m,则 的值为
的值为3.若函数 在
在 上单调递增,则实数
上单调递增,则实数 的取值范围是
的取值范围是______ .
 在
在 上单调递增,则实数
上单调递增,则实数 的取值范围是
的取值范围是4.已知数列 满足
满足 .则
.则 ___________.
___________.
 满足
满足 .则
.则 ___________.
___________.5.四棱锥P-ABCD中,已知侧面是边长为1的正三角形,M、N分别为边AB、BC的中点.则异面直线MN与PC之间的距离为___________.
6.设椭圆 的两个焦点为
的两个焦点为 ,过点
,过点 的直线与椭圆
的直线与椭圆 交于点P、Q.若
交于点P、Q.若 ,且
,且 ,则椭圆
,则椭圆 的短轴与长轴的比值为__________.
的短轴与长轴的比值为__________.
 的两个焦点为
的两个焦点为 ,过点
,过点 的直线与椭圆
的直线与椭圆 交于点P、Q.若
交于点P、Q.若 ,且
,且 ,则椭圆
,则椭圆 的短轴与长轴的比值为__________.
的短轴与长轴的比值为__________.7.设等边△ABC的内切圆半径为2、圆心为I.若点P满足PI=1,则△APB与△APC的面积之比的最大值为_________.
8.设A、B、C、D为空间四个不共面的点,以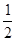 的概率在每对点之间连一条边,任意两对点之间是否连边是相互独立的,则点A与B可用(一条边或者若干条边组成的)空间折线连接的概率为_______.
的概率在每对点之间连一条边,任意两对点之间是否连边是相互独立的,则点A与B可用(一条边或者若干条边组成的)空间折线连接的概率为_______.
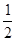 的概率在每对点之间连一条边,任意两对点之间是否连边是相互独立的,则点A与B可用(一条边或者若干条边组成的)空间折线连接的概率为_______.
的概率在每对点之间连一条边,任意两对点之间是否连边是相互独立的,则点A与B可用(一条边或者若干条边组成的)空间折线连接的概率为_______.9.在平面直角坐标系xOy中,P为不在x轴上的一个动点,且满足过点P可作抛物线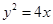 的两条切线,两切点连线
的两条切线,两切点连线 与PO垂直,直线
与PO垂直,直线 与PO、x轴的交点分别为Q、R.
与PO、x轴的交点分别为Q、R.
(1)证明:R为一个定点;
(2)求 的最小值.
的最小值.
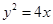 的两条切线,两切点连线
的两条切线,两切点连线 与PO垂直,直线
与PO垂直,直线 与PO、x轴的交点分别为Q、R.
与PO、x轴的交点分别为Q、R.(1)证明:R为一个定点;
(2)求
 的最小值.
的最小值.10.已知数列 满足
满足 .求正整数m使得
.求正整数m使得 .
.
 满足
满足 .求正整数m使得
.求正整数m使得 .
.11.确定所有的复数 ,使得对任意复数
,使得对任意复数 ,均有
,均有 .
.
 ,使得对任意复数
,使得对任意复数 ,均有
,均有 .
.12.设实数a、b、c满足 ,
, .证明:
.证明: .
.
 ,
, .证明:
.证明: .
.13.如图,在锐角△ABC中,∠BAC≠60°,过点B、C分别作△ABC外接圆的切线BD、CE,且满足 ,直线DE与AB、AC的延长线分别交于点F、G、CF与BD交于点M,CE与BG交于点N.证明:
,直线DE与AB、AC的延长线分别交于点F、G、CF与BD交于点M,CE与BG交于点N.证明: .
.
 ,直线DE与AB、AC的延长线分别交于点F、G、CF与BD交于点M,CE与BG交于点N.证明:
,直线DE与AB、AC的延长线分别交于点F、G、CF与BD交于点M,CE与BG交于点N.证明: .
.
14.设 .求最大的整数
.求最大的整数 ,使得集合S有k个互不相同的非空子集,具有性质:对这k个子集中任意两个不同子集,若它们的交非空,则它们交集中的最小元素与这两个子集中的最大元素均不相同.
,使得集合S有k个互不相同的非空子集,具有性质:对这k个子集中任意两个不同子集,若它们的交非空,则它们交集中的最小元素与这两个子集中的最大元素均不相同.
 .求最大的整数
.求最大的整数 ,使得集合S有k个互不相同的非空子集,具有性质:对这k个子集中任意两个不同子集,若它们的交非空,则它们交集中的最小元素与这两个子集中的最大元素均不相同.
,使得集合S有k个互不相同的非空子集,具有性质:对这k个子集中任意两个不同子集,若它们的交非空,则它们交集中的最小元素与这两个子集中的最大元素均不相同.15.设整数 模2014互不同余,整数
模2014互不同余,整数 模2014也互不同余.证明:可将
模2014也互不同余.证明:可将 重新排列为
重新排列为 ,使得
,使得 模4028互不同余.
模4028互不同余.
 模2014互不同余,整数
模2014互不同余,整数 模2014也互不同余.证明:可将
模2014也互不同余.证明:可将 重新排列为
重新排列为 ,使得
,使得 模4028互不同余.
模4028互不同余. 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
