全一卷
1.称{1,2,3,4,5,6,7,8,9}的某非空子集为奇子集:如果其中所有数之和为奇数,则奇子集的个数为____________ .
2.已知函数 的定义域为D.且点
的定义域为D.且点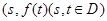 形成的图形为正方形,则实数a=
形成的图形为正方形,则实数a=____________ .
 的定义域为D.且点
的定义域为D.且点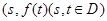 形成的图形为正方形,则实数a=
形成的图形为正方形,则实数a=3.等边三角形 与正方形
与正方形 有一公共边
有一公共边 ,二面角
,二面角 的余弦值为
的余弦值为 ,
, 分别是
分别是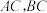 的中点,则
的中点,则 所成角的余弦值等于 .
所成角的余弦值等于 .
 与正方形
与正方形 有一公共边
有一公共边 ,二面角
,二面角 的余弦值为
的余弦值为 ,
, 分别是
分别是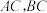 的中点,则
的中点,则 所成角的余弦值等于 .
所成角的余弦值等于 .4.在平面上, ,
,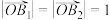 ,
, ,若
,若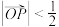 ,则
,则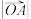 的取值范围是
的取值范围是________ .
 ,
,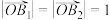 ,
, ,若
,若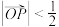 ,则
,则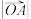 的取值范围是
的取值范围是5.等差数列{an}中,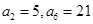 ,记数列
,记数列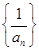 的前n项和为Sn,若
的前n项和为Sn,若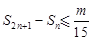 对任意的n∈N+恒成立,则正整数m的最小值为____________ .
对任意的n∈N+恒成立,则正整数m的最小值为____________ .
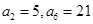 ,记数列
,记数列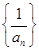 的前n项和为Sn,若
的前n项和为Sn,若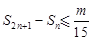 对任意的n∈N+恒成立,则正整数m的最小值为____________ .
对任意的n∈N+恒成立,则正整数m的最小值为____________ .6.计算: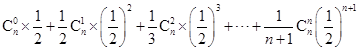 =____________ .
=____________ .
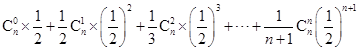 =____________ .
=____________ .7.如图,用6种不同的颜色给图中的4个格子涂色,每个格子涂一种颜色,要求最多使用3种颜色且相邻的两个格子颜色不同,则不同的涂色方法共有 种(用数字作答).


8.已知函数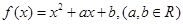 ,记M(a,b)是|f(x)|在区间[-1,1]上的最大值.当a、b满足M(a,b)≤2时,
,记M(a,b)是|f(x)|在区间[-1,1]上的最大值.当a、b满足M(a,b)≤2时, 的最大值为____________ .
的最大值为____________ .
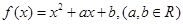 ,记M(a,b)是|f(x)|在区间[-1,1]上的最大值.当a、b满足M(a,b)≤2时,
,记M(a,b)是|f(x)|在区间[-1,1]上的最大值.当a、b满足M(a,b)≤2时, 的最大值为____________ .
的最大值为____________ .9.已知中心在原点,焦点在 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为 ,且经过点
,且经过点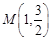 .
.
(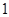 )求椭圆
)求椭圆 的方程.
的方程.
( )是否存在过点
)是否存在过点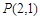 的直线
的直线 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点 ,
, ,满足
,满足 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为 ,且经过点
,且经过点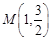 .
.(
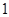 )求椭圆
)求椭圆 的方程.
的方程.(
 )是否存在过点
)是否存在过点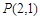 的直线
的直线 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点 ,
, ,满足
,满足 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.10.已知数列 中
中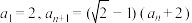 ,n=1,2,3,….
,n=1,2,3,….
(1)求 的通项公式;
的通项公式;
(2)若数列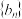 中
中 ,
,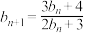 ,n=1,2,3,…证明:
,n=1,2,3,…证明: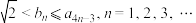 .
.
 中
中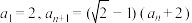 ,n=1,2,3,….
,n=1,2,3,….(1)求
 的通项公式;
的通项公式;(2)若数列
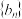 中
中 ,
,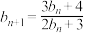 ,n=1,2,3,…证明:
,n=1,2,3,…证明: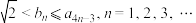 .
.11.锐角三角形ABC中,求证: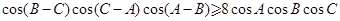 .
.
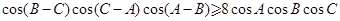 .
. 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
