全一卷
1.已知 ,
, ,且对任意
,且对任意 都有(1)
都有(1) ;(2)
;(2) .则
.则 的值为.
的值为.
 ,
, ,且对任意
,且对任意 都有(1)
都有(1) ;(2)
;(2) .则
.则 的值为.
的值为.A. | B. |
C. | D. |
2.已知函数 ,集合
,集合 ,
,  .则在平面直角坐标系内,集合
.则在平面直角坐标系内,集合 所表示区域的面积是.
所表示区域的面积是.
 ,集合
,集合 ,
,  .则在平面直角坐标系内,集合
.则在平面直角坐标系内,集合 所表示区域的面积是.
所表示区域的面积是.A. | B. | C.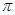 | D. |
3.一个正六面体的各个面和一个正八面体的各个面都是边长为 的正三角形,这样的两个多面体的内切球的半径之比是一个最简分数
的正三角形,这样的两个多面体的内切球的半径之比是一个最简分数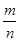 .那么,积
.那么,积 等于.
等于.
 的正三角形,这样的两个多面体的内切球的半径之比是一个最简分数
的正三角形,这样的两个多面体的内切球的半径之比是一个最简分数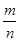 .那么,积
.那么,积 等于.
等于.| A.3 | B.4 | C.6 | D.12 |
4.设函数 满足下列条件:(1)
满足下列条件:(1) 是定义在
是定义在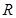 上的奇函数;(2)对任意的
上的奇函数;(2)对任意的 ,其中,常数
,其中,常数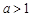 ,当
,当 时,有
时,有 .则下列不等式不一定成立的是.
.则下列不等式不一定成立的是.
 满足下列条件:(1)
满足下列条件:(1) 是定义在
是定义在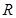 上的奇函数;(2)对任意的
上的奇函数;(2)对任意的 ,其中,常数
,其中,常数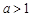 ,当
,当 时,有
时,有 .则下列不等式不一定成立的是.
.则下列不等式不一定成立的是.A. |
B. |
C. |
D. |
5.圆周上有十个等分点.则在以这十个等分点中的四个点为顶点的凸四边形中,梯形所占的比为.
A. | B. | C. | D. |
6.已知函数 则
则 ______.
______.
 则
则 ______.
______.7.不等式 对一切非零实数
对一切非零实数 均成立.则实数
均成立.则实数 的最大值是
的最大值是______ .
 对一切非零实数
对一切非零实数 均成立.则实数
均成立.则实数 的最大值是
的最大值是8.已知 ,点列
,点列 部分图像如图所示.则实数
部分图像如图所示.则实数 的值为______.
的值为______.
 ,点列
,点列 部分图像如图所示.则实数
部分图像如图所示.则实数 的值为______.
的值为______.
9.(1)若 (
( 、
、 为常数)对
为常数)对 恒成立,则常数
恒成立,则常数 的最小值为
的最小值为______ ;(2)对任意锐角 ,均有
,均有 成立,则
成立,则 的最大值为
的最大值为______ .
 (
( 、
、 为常数)对
为常数)对 恒成立,则常数
恒成立,则常数 的最小值为
的最小值为 ,均有
,均有 成立,则
成立,则 的最大值为
的最大值为10.已知 的半径为1,半径
的半径为1,半径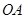 、
、 夹角为
夹角为 (
( ,
, 为常数),
为常数), 为圆上动点.若
为圆上动点.若 (
( ),则
),则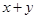 的最大值为
的最大值为______ .
 的半径为1,半径
的半径为1,半径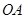 、
、 夹角为
夹角为 (
( ,
, 为常数),
为常数), 为圆上动点.若
为圆上动点.若 (
( ),则
),则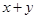 的最大值为
的最大值为11.以下是面点师工作环节的一个数学模型:
如图,在数轴上截取与闭区间 对应的线段,对折后(坐标4所对应的点与原点重合)再均匀地拉成4个单位长度的线段,这一过程称为一次操作(例如,在第一次操作完成后,原来的坐标l、3变成2,原来的坐标2变成4,等等).那么,原闭区间
对应的线段,对折后(坐标4所对应的点与原点重合)再均匀地拉成4个单位长度的线段,这一过程称为一次操作(例如,在第一次操作完成后,原来的坐标l、3变成2,原来的坐标2变成4,等等).那么,原闭区间 上(除两个端点外)的点,在第
上(除两个端点外)的点,在第 次操作完成后,恰好被拉到与4重合的点所对应的坐标为_______.
次操作完成后,恰好被拉到与4重合的点所对应的坐标为_______.
如图,在数轴上截取与闭区间
 对应的线段,对折后(坐标4所对应的点与原点重合)再均匀地拉成4个单位长度的线段,这一过程称为一次操作(例如,在第一次操作完成后,原来的坐标l、3变成2,原来的坐标2变成4,等等).那么,原闭区间
对应的线段,对折后(坐标4所对应的点与原点重合)再均匀地拉成4个单位长度的线段,这一过程称为一次操作(例如,在第一次操作完成后,原来的坐标l、3变成2,原来的坐标2变成4,等等).那么,原闭区间 上(除两个端点外)的点,在第
上(除两个端点外)的点,在第 次操作完成后,恰好被拉到与4重合的点所对应的坐标为_______.
次操作完成后,恰好被拉到与4重合的点所对应的坐标为_______.
12.(1)若 ,
, ,求证:
,求证: ;
;
(2)若 ,
, ,
, ,求证:
,求证: .
.
 ,
, ,求证:
,求证: ;
;(2)若
 ,
, ,
, ,求证:
,求证: .
.13.已知数列 满足
满足 (
( ,且
,且 ),前
),前 项和为
项和为 ,且
,且 .记
.记 .当
.当 时,问:是否存在正整数
时,问:是否存在正整数 ,使得对于任意正整数
,使得对于任意正整数 ,都有
,都有 ?如果存在,求出
?如果存在,求出 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
 满足
满足 (
( ,且
,且 ),前
),前 项和为
项和为 ,且
,且 .记
.记 .当
.当 时,问:是否存在正整数
时,问:是否存在正整数 ,使得对于任意正整数
,使得对于任意正整数 ,都有
,都有 ?如果存在,求出
?如果存在,求出 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.14.如图,四边形 的两条对角线交于点
的两条对角线交于点 ,
, 的平分线
的平分线 交线段
交线段 于点
于点 ,联结
,联结 ,作
,作 于点
于点 ,
, 于点
于点 ,且
,且 为边
为边 的中点,
的中点, .求证:
.求证: .
.
 的两条对角线交于点
的两条对角线交于点 ,
, 的平分线
的平分线 交线段
交线段 于点
于点 ,联结
,联结 ,作
,作 于点
于点 ,
, 于点
于点 ,且
,且 为边
为边 的中点,
的中点, .求证:
.求证: .
.
15.在平面直角坐标系内,画出同时满足以下条件的所有矩形:
(1)这些矩形的各边均与两坐标轴平行或重合;
(2)这些矩形的所有顶点(重复的只计算一次)恰好为100个整点(横、纵坐标均为整数的点称为整点).问:最多能画出多少个这样的矩形?说明你的理由.
(1)这些矩形的各边均与两坐标轴平行或重合;
(2)这些矩形的所有顶点(重复的只计算一次)恰好为100个整点(横、纵坐标均为整数的点称为整点).问:最多能画出多少个这样的矩形?说明你的理由.
 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
