搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．如果
，
，
，那么，
等于.
，
，
，那么，
等于.A． | B． | C． | D． |
2．已知
、
都是整数.命题甲：
不是偶数，则、都不是偶数；命题乙：不是偶数，则、不都是偶数.则.
、
都是整数.命题甲：
不是偶数，则、都不是偶数；命题乙：不是偶数，则、不都是偶数.则.| A．甲真，乙假 | B．甲假，乙真 |
| C．甲真，乙真 | D．甲假，乙假 |
3．若
、
是不共线的两个非零平面向量，则下面给出的四组、中，不共线的一组是
、
是不共线的两个非零平面向量，则下面给出的四组、中，不共线的一组是A． ， | B． ， |
C． ， | D． ， |
4．对定义在区间
上的函数
，若存在常数，对于任意的
有唯一的
，使得
，则称函数在 上的“均值”为.那么，函数
在
上的均值为.
上的函数
，若存在常数，对于任意的
有唯一的
，使得
，则称函数在 上的“均值”为.那么，函数
在
上的均值为.| A．10 | B． | C． | D． |
5．在三角形中，三条边长成等差数列是三边的比为3 ：4 ：5的.
| A．充分而不必要条件 | B．必要而不充分条件 |
| C．充分必要条件 | D．既不充分也不必要的条件 |
6．在平面直角坐标系中，横、纵坐标都是整数的点称为整点，如
就是一个整点.若直线
过点
和
，则在上与点
距离最近的整点是______.
就是一个整点.若直线
过点
和
，则在上与点
距离最近的整点是______.7．在
中，
，
.则
的最大值是______.
中，
，
.则
的最大值是______.8．2005个实数
满足
.则
的最小值等于______.
满足
.则
的最小值等于______.9．已知
.则函数
的最大值与最小值的和等于______ .
.则函数的最大值与最小值的和等于10．把单位正方体的六个面分别染上6种颜色，并画上个数不同的金鸡，各面的颜色与鸡的个数对应如表：
取同样的4个上述的单位正方体拼成一个如图所示的水平放置的长方体.则这个长方体的下底面总计画有______个金鸡
| 面上所染颜色 | 红 | 黄 | 蓝 | 青 | 紫 | 绿 |
| 该面上的金鸡个数 | 1 | 2 | 3 | 4 | 5 | 6 |
取同样的4个上述的单位正方体拼成一个如图所示的水平放置的长方体.则这个长方体的下底面总计画有______个金鸡
11．已知、、是实数，二次函数
满足
.求证：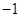
与1中至少有一个是
的根.
、、是实数，二次函数
满足
.求证：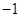
与1中至少有一个是
的根.12．圆内接凸四边形
的面积记为
， 
， 
，
， 
.证明：
（1）
，其中
；
（2）如果四边形同时具有外接圆和内切圆，则
.
的面积记为
， 
， 
，
， 
.证明：（1）
，其中
；（2）如果四边形
同时具有外接圆和内切圆，则
.13．设
个质数
构成公差为
的等差数列，且
.求证
（1）当是质数时，
；
（2）当
时，
.
个质数
构成公差为
的等差数列，且
.求证（1）当
是质数时，
；（2）当
时，
.