全一卷
1.若三位数 为平方数,其数字和
为平方数,其数字和 也为平方数,则称
也为平方数,则称 为“超级平方数”。这种超级平方数的个数为____________。
为“超级平方数”。这种超级平方数的个数为____________。
 为平方数,其数字和
为平方数,其数字和 也为平方数,则称
也为平方数,则称 为“超级平方数”。这种超级平方数的个数为____________。
为“超级平方数”。这种超级平方数的个数为____________。2.函数 的最大值为____________________。
的最大值为____________________。
 的最大值为____________________。
的最大值为____________________。3.设直线 过点
过点 .若直线
.若直线 被两平行线
被两平行线 与
与 所截得的线段长为
所截得的线段长为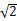 ,则直线
,则直线 的方程为________。
的方程为________。
 过点
过点 .若直线
.若直线 被两平行线
被两平行线 与
与 所截得的线段长为
所截得的线段长为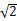 ,则直线
,则直线 的方程为________。
的方程为________。4.计算:
__________ .

5.满足 的实数
的实数 的取值范围是_____________。
的取值范围是_____________。
 的实数
的实数 的取值范围是_____________。
的取值范围是_____________。6.若实数 ,且
,且 ,
, ,则
,则 的取值范围是
的取值范围是__________ .
 ,且
,且 ,
, ,则
,则 的取值范围是
的取值范围是7.如图,正四面体 的各棱长均为2,
的各棱长均为2, 、
、 、
、 分别为棱
分别为棱 、
、 、
、 的中点,以
的中点,以 为圆心、1为半径,分别在面
为圆心、1为半径,分别在面 、面
、面 内作弧
内作弧 ,并将两弧各分成五等份,分点顺次为
,并将两弧各分成五等份,分点顺次为 、
、 、
、 、
、 、
、 、
、 以及
以及 、
、 、
、 、
、 、
、 、
、 .一只甲虫欲从点
.一只甲虫欲从点 出发,沿四面体表面爬行至点
出发,沿四面体表面爬行至点 ,则其爬行的最短距离为___________。
,则其爬行的最短距离为___________。
 的各棱长均为2,
的各棱长均为2, 、
、 、
、 分别为棱
分别为棱 、
、 、
、 的中点,以
的中点,以 为圆心、1为半径,分别在面
为圆心、1为半径,分别在面 、面
、面 内作弧
内作弧 ,并将两弧各分成五等份,分点顺次为
,并将两弧各分成五等份,分点顺次为 、
、 、
、 、
、 、
、 、
、 以及
以及 、
、 、
、 、
、 、
、 、
、 .一只甲虫欲从点
.一只甲虫欲从点 出发,沿四面体表面爬行至点
出发,沿四面体表面爬行至点 ,则其爬行的最短距离为___________。
,则其爬行的最短距离为___________。
8.在前一万个正整数构成的集合 中,被3除余2,且被5除余3、被7除余4的元素有______________个。
中,被3除余2,且被5除余3、被7除余4的元素有______________个。
 中,被3除余2,且被5除余3、被7除余4的元素有______________个。
中,被3除余2,且被5除余3、被7除余4的元素有______________个。9.正整数数列 满足
满足 ,
, .证明:数列的任何两项均互素。
.证明:数列的任何两项均互素。
 满足
满足 ,
, .证明:数列的任何两项均互素。
.证明:数列的任何两项均互素。10.如图, 为锐角
为锐角 的垂心,在线段
的垂心,在线段 上任取一点
上任取一点 ,延长
,延长 到点
到点 ,使
,使 ,作
,作 ⊥
⊥ 于点
于点 ,
, ⊥
⊥ 于点
于点 ,
, 为线段
为线段 的中点,
的中点, 、
、 分别为
分别为 的外接圆圆心、
的外接圆圆心、 的外接圆圆心,
的外接圆圆心, 与
与 的另一交点为
的另一交点为 .
.

证明:(1) 、
、 、
、 、
、 四点共圆;
四点共圆;
(2) 、
、 、
、 、
、 四点共圆.
四点共圆.
 为锐角
为锐角 的垂心,在线段
的垂心,在线段 上任取一点
上任取一点 ,延长
,延长 到点
到点 ,使
,使 ,作
,作 ⊥
⊥ 于点
于点 ,
, ⊥
⊥ 于点
于点 ,
, 为线段
为线段 的中点,
的中点, 、
、 分别为
分别为 的外接圆圆心、
的外接圆圆心、 的外接圆圆心,
的外接圆圆心, 与
与 的另一交点为
的另一交点为 .
.
证明:(1)
 、
、 、
、 、
、 四点共圆;
四点共圆;(2)
 、
、 、
、 、
、 四点共圆.
四点共圆.11.对于任意给定的无理数 、
、 及实数
及实数 ,证明:圆周
,证明:圆周 上至多只有两个有理点(纵、横坐标均为有理数的点)。
上至多只有两个有理点(纵、横坐标均为有理数的点)。
 、
、 及实数
及实数 ,证明:圆周
,证明:圆周 上至多只有两个有理点(纵、横坐标均为有理数的点)。
上至多只有两个有理点(纵、横坐标均为有理数的点)。12.从集合 中删去
中删去 个数,使得剩下的元素中,任两个数之和均不为2015的因数。求
个数,使得剩下的元素中,任两个数之和均不为2015的因数。求 的最小值。
的最小值。
 中删去
中删去 个数,使得剩下的元素中,任两个数之和均不为2015的因数。求
个数,使得剩下的元素中,任两个数之和均不为2015的因数。求 的最小值。
的最小值。 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
