全一卷
1.复数 满足
满足 ,且
,且 为纯虚数.则z=______.
为纯虚数.则z=______.
 满足
满足 ,且
,且 为纯虚数.则z=______.
为纯虚数.则z=______.2.方程 的解为______.
的解为______.
 的解为______.
的解为______.3.设函数 的最大值为
的最大值为 ,最小值为
,最小值为 ,则
,则 =
=___________ .
 的最大值为
的最大值为 ,最小值为
,最小值为 ,则
,则 =
=4.如图,  是半径为1的球的球心, 点A、B、C在球面上
是半径为1的球的球心, 点A、B、C在球面上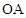 、
、 、
、 两两垂直,E、F分别为圆弧
两两垂直,E、F分别为圆弧 的中点.则点E、F在该球面上的球面距离为
的中点.则点E、F在该球面上的球面距离为______ .

 是半径为1的球的球心, 点A、B、C在球面上
是半径为1的球的球心, 点A、B、C在球面上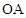 、
、 、
、 两两垂直,E、F分别为圆弧
两两垂直,E、F分别为圆弧 的中点.则点E、F在该球面上的球面距离为
的中点.则点E、F在该球面上的球面距离为
5.已知 且满足
且满足 .则
.则 的最大值为______
的最大值为______
 且满足
且满足 .则
.则 的最大值为______
的最大值为______6.将正整数数列 中的所有完全平方数去掉后,按原顺序构成数列
中的所有完全平方数去掉后,按原顺序构成数列 则
则 ______.
______.
 中的所有完全平方数去掉后,按原顺序构成数列
中的所有完全平方数去掉后,按原顺序构成数列 则
则 ______.
______.7.把1,2,…,6这六个数随机地排成一列组成一个数列,要求该数列恰先增后减.则这样的数列共有______个.
8.设 .若关于
.若关于 的方程
的方程 无实根,则实数
无实根,则实数 的取值范围是______.
的取值范围是______.
 .若关于
.若关于 的方程
的方程 无实根,则实数
无实根,则实数 的取值范围是______.
的取值范围是______.9.在△ABC中,  ,
,  .则
.则 ______.
______.
 ,
,  .则
.则 ______.
______.10.已知集合 .现随机选取
.现随机选取 中九个元素构成子集,记该子集中的最小数为
中九个元素构成子集,记该子集中的最小数为 ,则
,则 ______.
______.
 .现随机选取
.现随机选取 中九个元素构成子集,记该子集中的最小数为
中九个元素构成子集,记该子集中的最小数为 ,则
,则 ______.
______.11.证明:不存在这样的函数 ,满足对任意的整数x、y,若
,满足对任意的整数x、y,若 ,则
,则 .
.
 ,满足对任意的整数x、y,若
,满足对任意的整数x、y,若 ,则
,则 .
.12.对任意的x和正整数n,比较 和
和 的大小.
的大小.
 和
和 的大小.
的大小.13.已知椭圆 ,不过原点的直线
,不过原点的直线 与椭圆交于A、B两点.
与椭圆交于A、B两点.
(1)求 面积的最大值.
面积的最大值.
(2)是否存在椭圆 ,使得对于椭圆
,使得对于椭圆 的每一条切线与椭圆
的每一条切线与椭圆 均相交,设交于A、B两点,且
均相交,设交于A、B两点,且 恰取最大值?若存在,求出该椭圆;若不存在,说明理由.
恰取最大值?若存在,求出该椭圆;若不存在,说明理由.
 ,不过原点的直线
,不过原点的直线 与椭圆交于A、B两点.
与椭圆交于A、B两点.(1)求
 面积的最大值.
面积的最大值.(2)是否存在椭圆
 ,使得对于椭圆
,使得对于椭圆 的每一条切线与椭圆
的每一条切线与椭圆 均相交,设交于A、B两点,且
均相交,设交于A、B两点,且 恰取最大值?若存在,求出该椭圆;若不存在,说明理由.
恰取最大值?若存在,求出该椭圆;若不存在,说明理由.14.已知数列 满足
满足 .
.
(1)证明:当n≥2时, ;
;
(2)当n≥4时,求 表示不超过实数x的最大整数).
表示不超过实数x的最大整数).
 满足
满足 .
.(1)证明:当n≥2时,
 ;
;(2)当n≥4时,求
 表示不超过实数x的最大整数).
表示不超过实数x的最大整数). 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
