搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．设
．则
等于（ ）．
．则
等于（ ）．A． | B． |
C． | D． |
2．已知
、
是不等于1的正数，
．若
，则下面成立的是（ ）．
、
是不等于1的正数，
．若
，则下面成立的是（ ）．A． | B． |
C． | D． |
3．在
中，
则使等式
成立的充要条件是（ ）．
中，
则使等式
成立的充要条件是（ ）．A． | B． |
C． | D． |
4．抛物线顶点在原点，对称轴为
轴，焦点在直线
上．则抛物线方程为（ ）．
轴，焦点在直线
上．则抛物线方程为（ ）．A． | B． |
C． | D． |
5．设
．则二次曲线
与
必有（ ）．
．则二次曲线
与
必有（ ）．| A．不同的顶点 | B．不同的准线 |
| C．相同的焦点 | D．相同的离心率 |
6．设
适合等式
．则的值域是______．
适合等式
．则的值域是______．7．若对满足
的任何
都有
， 则数组
______．
的任何
都有
， 则数组
______．8．等差数列3，10，17，…，2005与3，8，13，…，2003中，值相同的项有______个．
9．设正数
，
满足
恒成立，则
的最小值是______ .
，
满足
恒成立，则
的最小值是10．若
为一个平方数，则正整数
______．
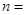为一个平方数，则正整数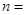
______．11．用标有1g，2g，3g，15g，40g的砝码各一个，在某架无刻度的天平上称量重物，如果天平两端均可放置砝码，那么，该天平所能称出的不同克数（正整数的重物）至多有______种．
12．如图，在
中，
分别是直角边
上的任意点，自点
向
引垂线，垂足分别是
．证明：四点共圆．
中，
分别是直角边
上的任意点，自点
向
引垂线，垂足分别是
．证明：四点共圆．
13．
的三条边长分别为
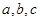．证明：
．
的三条边长分别为
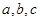．证明：
．14．试求最小的正整数
，使得对于任何个连续正整数中，必有一数，其各位数字之和是7的倍数．
，使得对于任何个连续正整数中，必有一数，其各位数字之和是7的倍数．