全一卷
1.一条直线 穿过一个四面体,则可同时与
穿过一个四面体,则可同时与 相交的四面体的面最多有( )个.
相交的四面体的面最多有( )个.
 穿过一个四面体,则可同时与
穿过一个四面体,则可同时与 相交的四面体的面最多有( )个.
相交的四面体的面最多有( )个.| A.1 | B.2 | C.3 | D.4 |
2.若偶函数 在
在 上是增函数,设
上是增函数,设 ,则
,则 的大小关系是( ).
的大小关系是( ).
 在
在 上是增函数,设
上是增函数,设 ,则
,则 的大小关系是( ).
的大小关系是( ).A. | B. | C. | D. |
3.设集合 ,
, .则
.则 中元素个数是( ).
中元素个数是( ).
 ,
, .则
.则 中元素个数是( ).
中元素个数是( ).| A.1 | B.2 | C.3 | D.4 |
4.设非零复数 满足
满足 ,以坐标原点为圆心,
,以坐标原点为圆心, 为半径作
为半径作 .则
.则 与
与 的关系是( ).
的关系是( ).
 满足
满足 ,以坐标原点为圆心,
,以坐标原点为圆心, 为半径作
为半径作 .则
.则 与
与 的关系是( ).
的关系是( ).| A.两点均在圆外 | B.两点均在圆内 | C.两点均在圆上 | D.一点在圆外,一点在圆内 |
5.方程 (
(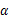 为
为 内异于
内异于 的常数的图形只能是( ).
的常数的图形只能是( ).
 (
(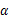 为
为 内异于
内异于 的常数的图形只能是( ).
的常数的图形只能是( ).A. | B. | C. | D. |
6.将所有与70互质的自然数由小到大排列,构成一数列 .则
.则 等于( ).
等于( ).
 .则
.则 等于( ).
等于( ).| A.568 | B.583 | C.638 | D.653 |
7.函数 的最小正周期是______.
的最小正周期是______.
 的最小正周期是______.
的最小正周期是______.8.设 ,且
,且 表示不超过
表示不超过 的最大整数.则
的最大整数.则 的值域是______.
的值域是______.
 ,且
,且 表示不超过
表示不超过 的最大整数.则
的最大整数.则 的值域是______.
的值域是______.9.在正三棱台 中,
中, ,截面
,截面 与
与 将三棱台分成三个棱锥
将三棱台分成三个棱锥 和
和 ,那么它们的体积
,那么它们的体积 之比为______.
之比为______.
 中,
中, ,截面
,截面 与
与 将三棱台分成三个棱锥
将三棱台分成三个棱锥 和
和 ,那么它们的体积
,那么它们的体积 之比为______.
之比为______.
10.用红、黄、蓝三色给正方体表面染色.每面只染一种颜色,每色各染两个面.如果经适当翻转可使两个染色的正方体各对应面颜色相同者视为一种,那么不同的染色方式有______种.
11.要使凸 边形的对角线相交成顶点在多边形内部的三角形的个数不少于1994,那么
边形的对角线相交成顶点在多边形内部的三角形的个数不少于1994,那么 最小应当是______.
最小应当是______.
 边形的对角线相交成顶点在多边形内部的三角形的个数不少于1994,那么
边形的对角线相交成顶点在多边形内部的三角形的个数不少于1994,那么 最小应当是______.
最小应当是______.12.设 .若方程
.若方程 的解为
的解为 ,则方程
,则方程 的解为______.
的解为______.
 .若方程
.若方程 的解为
的解为 ,则方程
,则方程 的解为______.
的解为______.13.在圆 上有两个动点
上有两个动点 和
和 ,且满足条件
,且满足条件 (
( 为坐标原点).求以
为坐标原点).求以 为邻边的矩形
为邻边的矩形 顶点
顶点 的轨迹方程.
的轨迹方程.
 上有两个动点
上有两个动点 和
和 ,且满足条件
,且满足条件 (
( 为坐标原点).求以
为坐标原点).求以 为邻边的矩形
为邻边的矩形 顶点
顶点 的轨迹方程.
的轨迹方程.14.将一个四面体的每个顶点与它所对底面三角形的重心相连接,得到4条线段.证明这4条线段相交于一点.
15.设复数 (
( )满足
)满足 .求
.求 的最大值、最小值及相应的z值.
的最大值、最小值及相应的z值.
 (
( )满足
)满足 .求
.求 的最大值、最小值及相应的z值.
的最大值、最小值及相应的z值.16.设集合 .如果
.如果 的一个二元子集
的一个二元子集 满足
满足 ,则称
,则称 具有性质
具有性质 .
.
(1)求 的具有性质
的具有性质 的所有二元子集的个数;
的所有二元子集的个数;
(2)求 的两两不相交具有性质
的两两不相交具有性质 的所有二元子集的个数.
的所有二元子集的个数.
 .如果
.如果 的一个二元子集
的一个二元子集 满足
满足 ,则称
,则称 具有性质
具有性质 .
.(1)求
 的具有性质
的具有性质 的所有二元子集的个数;
的所有二元子集的个数;(2)求
 的两两不相交具有性质
的两两不相交具有性质 的所有二元子集的个数.
的所有二元子集的个数.17.已知数列 中,
中, ,且当
,且当 时,
时, .试证:对
.试证:对 的一切自然数有
的一切自然数有 .
.
 中,
中, ,且当
,且当 时,
时, .试证:对
.试证:对 的一切自然数有
的一切自然数有 .
.18.已知平面四边形 中,
中, ,
, .求四边形
.求四边形 内一点到四条边各中点的距离之和的最小值.
内一点到四条边各中点的距离之和的最小值.
 中,
中, ,
, .求四边形
.求四边形 内一点到四条边各中点的距离之和的最小值.
内一点到四条边各中点的距离之和的最小值. 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
