全一卷
1.已知集合A={1,2,3,4},B={2,4,6,8},则A B中元素的个数为
B中元素的个数为
 B中元素的个数为
B中元素的个数为| A.1 | B.2 | C.3 | D.4 |
2.复平面内表示复数z=i(–2+i)的点位于
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
3.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.根据该折线图,下列结论错误的是( )


| A.月接待游客量逐月增加 |
| B.年接待游客量逐年增加 |
| C.各年的月接待游客量高峰期大致在7,8月 |
| D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳 |
4.已知 ,则
,则 .
.
 ,则
,则 .
.A. | B. | C. | D. |
5.设x,y满足约束条件 ,则z=x-y的取值范围是
,则z=x-y的取值范围是
 ,则z=x-y的取值范围是
,则z=x-y的取值范围是| A.[–3,0] | B.[–3,2] | C.[0,2] | D.[0,3] |
6.函数f(x)= sin(x+
sin(x+ )+cos(x−
)+cos(x− )的最大值为
)的最大值为
 sin(x+
sin(x+ )+cos(x−
)+cos(x− )的最大值为
)的最大值为A. | B.1 | C. | D. |
7.函数 的部分图像大致为( )
的部分图像大致为( )
 的部分图像大致为( )
的部分图像大致为( )A. | B. |
C. | D. |
8.执行下面的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为


| A.5 | B.4 | C.3 | D.2 |
9.(2017新课标全国Ⅲ理科)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为
A. | B. |
C. | D. |
10.在正方体 中,
中, 为棱
为棱 的中点,则.
的中点,则.
 中,
中, 为棱
为棱 的中点,则.
的中点,则.A. | B. | C. | D. |
11.(2017新课标全国卷Ⅲ文科)已知椭圆C: 的左、右顶点分别为A1,A2,且以线段A1A2为直径的圆与直线
的左、右顶点分别为A1,A2,且以线段A1A2为直径的圆与直线 相切,则C的离心率为
相切,则C的离心率为
 的左、右顶点分别为A1,A2,且以线段A1A2为直径的圆与直线
的左、右顶点分别为A1,A2,且以线段A1A2为直径的圆与直线 相切,则C的离心率为
相切,则C的离心率为A. | B. |
C. | D. |
12.已知函数 有唯一零点,则
有唯一零点,则
 有唯一零点,则
有唯一零点,则
A. | B. | C. | D.1 |
13.已知向量 ,且
,且 ,则
,则
_______ .
 ,且
,且 ,则
,则
14.(2017新课标全国III文科)双曲线 (a>0)的一条渐近线方程为
(a>0)的一条渐近线方程为 ,则a=______________.
,则a=______________.
 (a>0)的一条渐近线方程为
(a>0)的一条渐近线方程为 ,则a=______________.
,则a=______________.15.△ABC的内角A,B,C的对边分别为a,b,c.已知C=60°,b=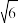 ,c=3,则A=
,c=3,则A=_________ .
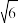 ,c=3,则A=
,c=3,则A=16.设函数 则满足
则满足 的x的取值范围是
的x的取值范围是____________ .
 则满足
则满足 的x的取值范围是
的x的取值范围是17.设数列 满足
满足 .
.
(1)求 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和.
项和.
 满足
满足 .
.(1)求
 的通项公式;
的通项公式;(2)求数列
 的前
的前 项和.
项和.18.某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)求六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.
最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
(1)求六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.
19.如图,四面体ABCD中,△ABC是正三角形,AD=CD.


(1)证明:AC⊥BD;
(2)已知△ACD是直角三角形,AB=BD.若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.
20.在直角坐标系xOy中,曲线 与x轴交于A,B两点,点C的坐标为
与x轴交于A,B两点,点C的坐标为 .当m变化时,解答下列问题:
.当m变化时,解答下列问题:
(1)能否出现AC⊥BC的情况?说明理由;
(2)证明过A,B,C三点的圆在y轴上截得的弦长为定值.
 与x轴交于A,B两点,点C的坐标为
与x轴交于A,B两点,点C的坐标为 .当m变化时,解答下列问题:
.当m变化时,解答下列问题:(1)能否出现AC⊥BC的情况?说明理由;
(2)证明过A,B,C三点的圆在y轴上截得的弦长为定值.
21.已知函数 .
.
(1)讨论 的单调性;
的单调性;
(2)当 时,证明
时,证明 .
.
 .
.(1)讨论
 的单调性;
的单调性;(2)当
 时,证明
时,证明 .
.22.
在直角坐标系xOy中,直线l1的参数方程为 (t为参数),直线l2的参数方程为
(t为参数),直线l2的参数方程为 .设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
.设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
(1)写出C的普通方程;
(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设 ,M为l3与C的交点,求M的极径.
,M为l3与C的交点,求M的极径.
在直角坐标系xOy中,直线l1的参数方程为
 (t为参数),直线l2的参数方程为
(t为参数),直线l2的参数方程为 .设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
.设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.(1)写出C的普通方程;
(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设
 ,M为l3与C的交点,求M的极径.
,M为l3与C的交点,求M的极径.23.已知函数 =│x+1│–│x–2│.
=│x+1│–│x–2│.
(1)求不等式 ≥1的解集;
≥1的解集;
(2)若不等式 ≥x2–x +m的解集非空,求实数m的取值范围.
≥x2–x +m的解集非空,求实数m的取值范围.
 =│x+1│–│x–2│.
=│x+1│–│x–2│.(1)求不等式
 ≥1的解集;
≥1的解集;(2)若不等式
 ≥x2–x +m的解集非空,求实数m的取值范围.
≥x2–x +m的解集非空,求实数m的取值范围. 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
