搜索
全一卷
难度系数：0.64 
答案解析
有奖纠错
1．已知集合
，则
，则
A． | B． | C． | D． |
2．复数
| A．i | B．1+i | C． | D． |
3．执行如图所示的程序框图，输出的s值为
| A．8 | B．9 | C．27 | D．36 |
4．下列函数中，在区间
上为减函数的是
上为减函数的是A． | B． | C． | D． |
5．圆（x+1）2+y2=2的圆心到直线y=x+3的距离为
| A．1 | B．2 | C． | D．2 |
6．从甲、乙等5名学生中随机选出2人，则甲被选中的概率为
A． | B． | C． | D． |
7．已知A（2,5），B（4,1）.若点P（x,y）在线段AB上，则2x−y的最大值为
| A．−1 | B．3 | C．7 | D．8 |
8．某学校运动会的立定跳远和30秒跳绳两个单项比赛分成预赛和决赛两个阶段.下表为10名学生的预赛成绩，其中有三个数据模糊.
在这10名学生中，进入立定跳远决赛的有8人，同时进入立定跳远决赛和30秒跳绳决赛的有6人，则
（A）2号学生进入30秒跳绳决赛
（B）5号学生进入30秒跳绳决赛
（C）8号学生进入30秒跳绳决赛
（D）9号学生进入30秒跳绳决赛
| 学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 立定跳远（单位：米） | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
| 30秒跳绳（单位：次） | 63 | a | 75 | 60 | 63 | 72 | 70 | a−1 | b | 65 |
（A）2号学生进入30秒跳绳决赛
（B）5号学生进入30秒跳绳决赛
（C）8号学生进入30秒跳绳决赛
（D）9号学生进入30秒跳绳决赛
9．已知向量
，则a与b夹角的大小为_________.
，则a与b夹角的大小为_________.10．函数
的最大值为_________.
的最大值为_________.11．某四棱柱的三视图如图所示，则该四棱柱的体积为___________.
12．已知双曲线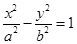
（a＞0，b＞0）的一条渐近线为2x+y=0，一个焦点为（
,0），则a=_______；b=_______.
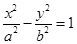（a＞0，b＞0）的一条渐近线为2x+y=0，一个焦点为（
,0），则a=_______；b=_______.13．在△ABC中，
，a=
c，则
=_________.
，a=
c，则
=_________.14．某网店统计了连续三天售出商品的种类情况：第一天售出19种商品，第二天售出13种商品，第三天售出18种商品；前两天都售出的商品有3种，后两天都售出的商品有4种，则该网店
①第一天售出但第二天未售出的商品有______种；
②这三天售出的商品最少有_______种.
①第一天售出但第二天未售出的商品有______种；
②这三天售出的商品最少有_______种.
15．已知{an}是等差数列，{bn}是等比数列，且b2=3，b3=9，a1=b1，a14=b4.
（Ⅰ）求{an}的通项公式；
（Ⅱ）设cn= an+ bn，求数列{cn}的前n项和.
（Ⅰ）求{an}的通项公式；
（Ⅱ）设cn= an+ bn，求数列{cn}的前n项和.
16．已知函数f（x）="2sin" ωx cos ωx+ cos 2ωx（ω>0）的最小正周期为π.
（Ⅰ）求ω的值；
（Ⅱ）求f（x）的单调递增区间.
（Ⅰ）求ω的值；
（Ⅱ）求f（x）的单调递增区间.
17．某市居民用水拟实行阶梯水价，每人月用水量中不超过w立方米的部分按4元/立方米收费，超出w立方米的部分按10元/立方米收费.从该市随机调查了10 000位居民，获得了他们某月的用水量数据，整理得到如下频率分布直方图：
（Ⅰ）如果w为整数，那么根据此次调查，为使80%以上居民在该月的用水价格为4元/立方米，w至少定为多少？
（Ⅱ）假设同组中的每个数据用该组区间的右端点值代替，当w=3时，估计该市居民该月的人均水费.
（Ⅰ）如果w为整数，那么根据此次调查，为使80%以上居民在该月的用水价格为4元/立方米，w至少定为多少？
（Ⅱ）假设同组中的每个数据用该组区间的右端点值代替，当w=3时，估计该市居民该月的人均水费.
18．如图，在四棱锥
中，
平面
，
.
（Ⅰ）求证：
；
（Ⅱ）求证：
；
（Ⅲ）设点E为AB的中点，在棱PB上是否存在点F，使得
平面
?说明理由.
中，平面，.（Ⅰ）求证：
；（Ⅱ）求证：
；（Ⅲ）设点E为AB的中点，在棱PB上是否存在点F，使得
平面?说明理由.19．已知椭圆C：
过A（2,0），B（0,1）两点.
（Ⅰ）求椭圆C的方程及离心率；
（Ⅱ）设P为第三象限内一点且在椭圆C上，直线PA与y轴交于点M，直线PB与x轴交于点N，求证：四边形ABNM的面积为定值.
过A（2,0），B（0,1）两点.（Ⅰ）求椭圆C的方程及离心率；
（Ⅱ）设P为第三象限内一点且在椭圆C上，直线PA与y轴交于点M，直线PB与x轴交于点N，求证：四边形ABNM的面积为定值.
20．设函数
（Ⅰ）求曲线
在点
处的切线方程；
（Ⅱ）设
，若函数
有三个不同零点，求c的取值范围；
（Ⅲ）求证：
是有三个不同零点的必要而不充分条件.
（Ⅰ）求曲线
在点处的切线方程；（Ⅱ）设
，若函数有三个不同零点，求c的取值范围；（Ⅲ）求证：
是有三个不同零点的必要而不充分条件.