搜索
全一卷
难度系数：0.85 
答案解析
有奖纠错
1．已知集合A=
，B=
，则
，B=
，则A．A B= | B．AB |
C．A B | D．AB=R |
2．为评估一种农作物的种植效果，选了n块地作试验田．这n块地的亩产量（单位：kg）分别为x1，x2，…，xn，下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是
| A．x1，x2，…，xn的平均数 | B．x1，x2，…，xn的标准差 |
| C．x1，x2，…，xn的最大值 | D．x1，x2，…，xn的中位数 |
3．下列各式的运算结果为纯虚数的是
A． | B． | C． | D． |
4．如图，正方形
内的图形来自中国古代的太极图，正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称，在正方形内随机取一点，则此点取自黑色部分的概率是（ ）．
内的图形来自中国古代的太极图，正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称，在正方形内随机取一点，则此点取自黑色部分的概率是（ ）．
A． | B． | C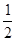． | D． |
5．已知F是双曲线C：
的右焦点，P是C上一点，且PF与x轴垂直，点A的坐标是(1，3)，则
的面积为
的右焦点，P是C上一点，且PF与x轴垂直，点A的坐标是(1，3)，则
的面积为A． | B． |
C． | D． |
6．如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ不平行的是( )
A． | B． |
C． | D． |
7．设x，y满足约束条件
则z=x+y的最大值为（ ）
则z=x+y的最大值为（ ）| A．0 | B．1 | C．2 | D．3 |
8．函数
的部分图像大致为
的部分图像大致为A． | B． | C． | D． |
9．已知函数
，则
，则A． 在（0，2）单调递增 | B．在（0，2）单调递减 |
C． 的图像关于直线x=1对称 | D．的图像关于点（1，0）对称 |
10．如图是为了求出满足
的最小偶数
，那么在
和
两个空白框中，可以分别填入( )
的最小偶数
，那么在
和
两个空白框中，可以分别填入( )
A． 和 | B．和 |
C． 和 | D．和 |
11．△ABC的内角A、B、C的对边分别为a、b、c．已知
，a=2，c=
，则C=
，a=2，c=，则C=A． | B． | C． | D． |
12．（2017新课标全国卷Ⅰ文科）设A，B是椭圆C：
长轴的两个端点，若C上存在点M满足∠AMB=120°，则m的取值范围是
长轴的两个端点，若C上存在点M满足∠AMB=120°，则m的取值范围是A． | B． |
C． | D． |
13．已知向量
=（﹣1，2），
=（m，1），若
，则m=_________ ．
=（﹣1，2），
=（m，1），若
，则m=14．曲线
在点（1，2）处的切线方程为______________ ．
在点（1，2）处的切线方程为15．已知
，tanα=2，则
=______________ ．
，tanα=2，则=16．已知三棱锥
的所有顶点都在球O的球面上，SC是球O的直径
若平面
平面SCB，
，
，三棱锥的体积为9，则球O的表面积为______．
的所有顶点都在球O的球面上，SC是球O的直径
若平面
平面SCB，
，
，三棱锥的体积为9，则球O的表面积为______．17．记Sn为等比数列
的前n项和，已知S2=2，S3=-6.
（1）求的通项公式；
（2）求Sn，并判断Sn+1，Sn，Sn+2是否成等差数列．
的前n项和，已知S2=2，S3=-6.（1）求
的通项公式；（2）求Sn，并判断Sn+1，Sn，Sn+2是否成等差数列．
18．如图，在四棱锥
中，
，且
.
（1）证明：平面
平面
；
（2）若
，
，且四棱锥的体积为
，求该四棱锥的侧面积．
中，，且.（1）证明：平面
平面；（2）若
，，且四棱锥的体积为，求该四棱锥的侧面积．19．为了监控某种零件的一条生产线的生产过程，检验员每隔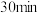
从该生产线上随机抽取一个零件，并测量其尺寸（单位：
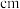）．下面是检验员在一天内依次抽取的16个零件的尺寸：
经计算得
，
，
，其中
为抽取的第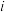
个零件的尺寸，
．
（1）求
的相关系数
，并回答是否可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小（若
，则可以认为零件的尺寸不随生产过程的进行而系统地变大或变小）．
（2）一天内抽检零件中，如果出现了尺寸在
之外的零件，就认为这条生产线在这一天的生产过程可能出现了异常情况，需对当天的生产过程进行检查．
（ⅰ）从这一天抽检的结果看，是否需对当天的生产过程进行检查？
（ⅱ）在之外的数据称为离群值，试剔除离群值，估计这条生产线当天生产的零件尺寸的均值与标准差．（精确到
）附：样本
的相关系数
，
．
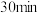从该生产线上随机抽取一个零件，并测量其尺寸（单位：
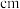）．下面是检验员在一天内依次抽取的16个零件的尺寸：| 抽取次序 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 零件尺寸 | 9．95 | 10．12 | 9．96 | 9．96 | 10．01 | 9．92 | 9．98 | 10．04 |
| 抽取次序 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 零件尺寸 | 10．26 | 9．91 | 10．13 | 10．02 | 9．22 | 10．04 | 10．05 | 9．95 |
经计算得
，
，
，其中
为抽取的第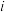
个零件的尺寸，
．（1）求
的相关系数
，并回答是否可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小（若
，则可以认为零件的尺寸不随生产过程的进行而系统地变大或变小）．（2）一天内抽检零件中，如果出现了尺寸在
之外的零件，就认为这条生产线在这一天的生产过程可能出现了异常情况，需对当天的生产过程进行检查．（ⅰ）从这一天抽检的结果看，是否需对当天的生产过程进行检查？
（ⅱ）在
之外的数据称为离群值，试剔除离群值，估计这条生产线当天生产的零件尺寸的均值与标准差．（精确到
）附：样本
的相关系数
，
．20．设
、
为曲线
：
上两点，与的横坐标之和为
．
（1）求直线
的斜率；
（2）
为曲线上一点，在处的切线与直线平行，且
，求直线的方程．
、
为曲线
：
上两点，与的横坐标之和为
．（1）求直线
的斜率；（2）
为曲线上一点，在处的切线与直线平行，且
，求直线的方程．21．已知函数
．
（1）讨论
的单调性；
（2）若
，求
的取值范围．
．（1）讨论
的单调性；（2）若
，求
的取值范围．22．在直角坐标系xOy中，曲线C的参数方程为
（θ为参数），直线l的参数方程为
．
（1）若
，求C与l的交点坐标；
（2）若C上的点到l的距离的最大值为
，求
．
（θ为参数），直线l的参数方程为
．（1）若
，求C与l的交点坐标；（2）若C上的点到l的距离的最大值为
，求
．23．已知函数
，
．
（1）当
时，求不等式
的解集；
（2）若不等式的解集包含[–1，1]，求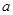
的取值范围．
，
．（1）当
时，求不等式
的解集；（2）若不等式
的解集包含[–1，1]，求
的取值范围．