全一卷
1.在平面直角坐标系 中,点
中,点 、
、 在抛物线
在抛物线 上,满足
上,满足 ,
, 为抛物线的焦点. 则
为抛物线的焦点. 则 的最小值为
的最小值为______ .
 中,点
中,点 、
、 在抛物线
在抛物线 上,满足
上,满足 ,
, 为抛物线的焦点. 则
为抛物线的焦点. 则 的最小值为
的最小值为2.集合 是由
是由 中的40个元素组成的子集,
中的40个元素组成的子集, 为集合
为集合 中的所有元素之和,则
中的所有元素之和,则 的取值个数为______.
的取值个数为______.
 是由
是由 中的40个元素组成的子集,
中的40个元素组成的子集, 为集合
为集合 中的所有元素之和,则
中的所有元素之和,则 的取值个数为______.
的取值个数为______.3.将集合 中的数从小到大排列,则第60个数为______(用数字作答).
中的数从小到大排列,则第60个数为______(用数字作答).
 中的数从小到大排列,则第60个数为______(用数字作答).
中的数从小到大排列,则第60个数为______(用数字作答).4.已知数列 满足
满足 ,
, ,则
,则 ______.
______.
 满足
满足 ,
, ,则
,则 ______.
______.5.在 中,
中, ,
, ,
, ,
, 为
为 的中点. 将
的中点. 将 沿
沿 折起,使
折起,使 、
、 两点间的距离为
两点间的距离为 . 则点
. 则点 到平面
到平面 的距离为______.
的距离为______.
 中,
中, ,
, ,
, ,
, 为
为 的中点. 将
的中点. 将 沿
沿 折起,使
折起,使 、
、 两点间的距离为
两点间的距离为 . 则点
. 则点 到平面
到平面 的距离为______.
的距离为______.6.函数 的最大值为______.
的最大值为______.
 的最大值为______.
的最大值为______.7.在一个圆上随机取三点,则以此三点为顶点的三角形是锐角三角形的概率为______.
8.设 的
的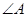 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,且满足
,且满足 . 则
. 则 ______.
______.
 的
的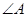 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,且满足
,且满足 . 则
. 则 ______.
______.9.已知复数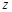 满足
满足 . 求
. 求 的最大值.
的最大值.
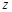 满足
满足 . 求
. 求 的最大值.
的最大值.10.设过原点且斜率为正值的直线与椭圆 交于点
交于点 、
、 ,点
,点 ,
, . 求四边形
. 求四边形 面积的最大值.
面积的最大值.
 交于点
交于点 、
、 ,点
,点 ,
, . 求四边形
. 求四边形 面积的最大值.
面积的最大值.11.设 为一个含有
为一个含有 个元素的集合,
个元素的集合, 为集合
为集合 的互不相同的
的互不相同的 个子集. 证明:在集合
个子集. 证明:在集合 中存在一个元素
中存在一个元素 ,使得
,使得 ,
, ,…,
,…, 仍为互不相同的集合,其中,
仍为互不相同的集合,其中, .
.
 为一个含有
为一个含有 个元素的集合,
个元素的集合, 为集合
为集合 的互不相同的
的互不相同的 个子集. 证明:在集合
个子集. 证明:在集合 中存在一个元素
中存在一个元素 ,使得
,使得 ,
, ,…,
,…, 仍为互不相同的集合,其中,
仍为互不相同的集合,其中, .
. 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
