全一卷
1.设集合 ,则
,则
 ,则
,则
A. | B. | C. | D. |
2.设 ,则“
,则“ ”是“
”是“ ”的( )
”的( )
 ,则“
,则“ ”是“
”是“ ”的( )
”的( )| A.充要条件 | B.充分而不必要条件 |
| C.必要而不充分条件 | D.既不充分也不必要条件 |
3.有5支彩笔(除颜色外无差别),颜色分别为红、黄、蓝、绿、紫.从这5支彩笔中任取2支不同颜色的彩笔,则取出的2支彩笔中含有红色彩笔的概率为
A. | B. | C.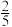 | D.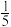 |
4.阅读下面的程序框图,运行相应的程序,若输入 的值为19,则输出
的值为19,则输出 的值为( )
的值为( )

 的值为19,则输出
的值为19,则输出 的值为( )
的值为( )
| A.0 | B.1 | C.2 | D.3 |
5.【陕西省西安市长安区第一中学上学期期末考】已知双曲线 的左焦点为
的左焦点为 ,点
,点 在双曲线的渐近线上,
在双曲线的渐近线上, 是边长为2的等边三角形(
是边长为2的等边三角形( 为原点),则双曲线的方程为( )
为原点),则双曲线的方程为( )
 的左焦点为
的左焦点为 ,点
,点 在双曲线的渐近线上,
在双曲线的渐近线上, 是边长为2的等边三角形(
是边长为2的等边三角形( 为原点),则双曲线的方程为( )
为原点),则双曲线的方程为( )A. | B. | C. | D. |
6.已知奇函数 在
在 上是增函数,若
上是增函数,若 ,
, ,
, ,则
,则 的大小关系为
的大小关系为
 在
在 上是增函数,若
上是增函数,若 ,
, ,
, ,则
,则 的大小关系为
的大小关系为A. | B. | C. | D. |
7.设函数 ,
, ,其中
,其中 ,
, .若
.若 ,
, ,且
,且 的最小正周期大于
的最小正周期大于 ,则
,则
 ,
, ,其中
,其中 ,
, .若
.若 ,
, ,且
,且 的最小正周期大于
的最小正周期大于 ,则
,则A. , , | B. , , | C. , , | D. , , |
8.已知函数 .设
.设 ,若关于
,若关于 的不等式
的不等式 在
在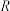 上恒成立,则
上恒成立,则 的取值范围是
的取值范围是
 .设
.设 ,若关于
,若关于 的不等式
的不等式 在
在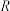 上恒成立,则
上恒成立,则 的取值范围是
的取值范围是A. | B. |
C. | D. |
9.已知 ,
,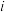 为虚数单位,若
为虚数单位,若 为实数,则
为实数,则 的值为
的值为__________ .
 ,
,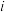 为虚数单位,若
为虚数单位,若 为实数,则
为实数,则 的值为
的值为10.已知 ,设函数
,设函数 的图象在点(1,
的图象在点(1, )处的切线为l,则l在y轴上的截距为
)处的切线为l,则l在y轴上的截距为________ .
 ,设函数
,设函数 的图象在点(1,
的图象在点(1, )处的切线为l,则l在y轴上的截距为
)处的切线为l,则l在y轴上的截距为11.
已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为
12.设抛物线 的焦点为F,准线为l.已知点C在l上,以C为圆心的圆与y轴的正半轴相切于点A.若
的焦点为F,准线为l.已知点C在l上,以C为圆心的圆与y轴的正半轴相切于点A.若 ,则圆的方程为
,则圆的方程为____________ .
 的焦点为F,准线为l.已知点C在l上,以C为圆心的圆与y轴的正半轴相切于点A.若
的焦点为F,准线为l.已知点C在l上,以C为圆心的圆与y轴的正半轴相切于点A.若 ,则圆的方程为
,则圆的方程为13.若 ,
, ,则
,则 的最小值为
的最小值为___________ .
 ,
, ,则
,则 的最小值为
的最小值为14.在 中,
中, ,
,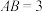 ,
, . 若
. 若 ,
, ,且
,且 ,则
,则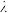 的值为
的值为______________ .
 中,
中, ,
,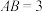 ,
, . 若
. 若 ,
, ,且
,且 ,则
,则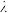 的值为
的值为15.在 中,内角
中,内角 所对的边分别为
所对的边分别为 .已知
.已知 ,
, .
.
(I)求 的值;
的值;
(II)求 的值.
的值.
 中,内角
中,内角 所对的边分别为
所对的边分别为 .已知
.已知 ,
, .
.(I)求
 的值;
的值;(II)求
 的值.
的值.16.电视台播放甲、乙两套连续剧,每次播放连续剧时,需要播放广告.已知每次播放甲、乙两套连续剧时,连续剧播放时长、广告播放时长、收视人次如下表所示:
已知电视台每周安排的甲、乙连续剧的总播放时间不多于600分钟,广告的总播放时间不少于30分钟,且甲连续剧播放的次数不多于乙连续剧播放次数的2倍.分别用 ,
,  表示每周计划播出的甲、乙两套连续剧的次数.
表示每周计划播出的甲、乙两套连续剧的次数.
(I)用 ,
, 列出满足题目条件的数学关系式,并画出相应的平面区域;
列出满足题目条件的数学关系式,并画出相应的平面区域;
(II)问电视台每周播出甲、乙两套连续剧各多少次,才能使收视人次最多?
| 连续剧播放时长(分钟) | 广告播放时长(分钟) | 收视人次(万) |
甲 | 70 | 5 | 60 |
乙 | 60 | 5 | 25 |
 ,
,  表示每周计划播出的甲、乙两套连续剧的次数.
表示每周计划播出的甲、乙两套连续剧的次数.(I)用
 ,
, 列出满足题目条件的数学关系式,并画出相应的平面区域;
列出满足题目条件的数学关系式,并画出相应的平面区域;(II)问电视台每周播出甲、乙两套连续剧各多少次,才能使收视人次最多?
17.如图,在四棱锥 中,
中, 平面
平面 ,
, ,
, ,
, ,
, ,
, ,
, .
.
(I)求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(II)求证: 平面
平面 ;
;
(Ⅲ)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.

 中,
中, 平面
平面 ,
, ,
, ,
, ,
, ,
, ,
, .
.(I)求异面直线
 与
与 所成角的余弦值;
所成角的余弦值;(II)求证:
 平面
平面 ;
;(Ⅲ)求直线
 与平面
与平面 所成角的正弦值.
所成角的正弦值.
18.已知 为等差数列,前n项和为
为等差数列,前n项和为 ,
, 是首项为2的等比数列,且公比大于0,
是首项为2的等比数列,且公比大于0,
 .
.
(Ⅰ)求 和
和 的通项公式;
的通项公式;
(Ⅱ)求数列 的前n项和
的前n项和 .
.
 为等差数列,前n项和为
为等差数列,前n项和为 ,
, 是首项为2的等比数列,且公比大于0,
是首项为2的等比数列,且公比大于0, .
.(Ⅰ)求
 和
和 的通项公式;
的通项公式;(Ⅱ)求数列
 的前n项和
的前n项和 .
.19.设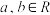 ,
, .已知函数
.已知函数 ,
, .
.
(Ⅰ)求 的单调区间;
的单调区间;
(Ⅱ)已知函数 和
和 的图象在公共点(x0,y0)处有相同的切线,
的图象在公共点(x0,y0)处有相同的切线,
(i)求证: 在
在 处的导数等于0;
处的导数等于0;
(ii)若关于x的不等式 在区间
在区间 上恒成立,求b的取值范围.
上恒成立,求b的取值范围.
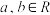 ,
, .已知函数
.已知函数 ,
, .
.(Ⅰ)求
 的单调区间;
的单调区间;(Ⅱ)已知函数
 和
和 的图象在公共点(x0,y0)处有相同的切线,
的图象在公共点(x0,y0)处有相同的切线,(i)求证:
 在
在 处的导数等于0;
处的导数等于0;(ii)若关于x的不等式
 在区间
在区间 上恒成立,求b的取值范围.
上恒成立,求b的取值范围.20.已知椭圆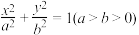 的左焦点为
的左焦点为 ,右顶点为
,右顶点为 ,点
,点 的坐标为
的坐标为 ,
, 的面积为
的面积为 .
.
(I)求椭圆的离心率;
(II)设点 在线段
在线段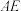 上,
上, ,延长线段
,延长线段 与椭圆交于点
与椭圆交于点 ,点
,点 ,
, 在
在 轴上,
轴上, ,且直线
,且直线 与直线
与直线 间的距离为
间的距离为 ,四边形
,四边形 的面积为
的面积为 .
.
(i)求直线 的斜率;
的斜率;
(ii)求椭圆的方程.
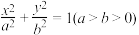 的左焦点为
的左焦点为 ,右顶点为
,右顶点为 ,点
,点 的坐标为
的坐标为 ,
, 的面积为
的面积为 .
.(I)求椭圆的离心率;
(II)设点
 在线段
在线段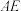 上,
上, ,延长线段
,延长线段 与椭圆交于点
与椭圆交于点 ,点
,点 ,
, 在
在 轴上,
轴上, ,且直线
,且直线 与直线
与直线 间的距离为
间的距离为 ,四边形
,四边形 的面积为
的面积为 .
.(i)求直线
 的斜率;
的斜率;(ii)求椭圆的方程.
 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
