全一卷
1.设集合 ,
, ,则
,则 ( )
( )
 ,
, ,则
,则 ( )
( )A. | B. | C. | D. |
2.设 ,其中x,y是实数,则
,其中x,y是实数,则
 ,其中x,y是实数,则
,其中x,y是实数,则
| A.1 | B. | C. | D.2 |
3.已知等差数列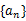 前9项的和为27,
前9项的和为27, ,则
,则
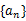 前9项的和为27,
前9项的和为27, ,则
,则
| A.100 | B.99 | C.98 | D.97 |
4.某公司的班车在7:30,8:00,8:30发车,小明在7:50至8:30之间到达发车站乘坐班车,且到达发车站的时刻是随机的,则他等车时间不超过10分钟的概率是
A. | B. | C.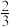 | D.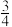 |
5.已知方程 表示双曲线,且该双曲线两焦点间的距离为4,则n的取值范围是
表示双曲线,且该双曲线两焦点间的距离为4,则n的取值范围是
 表示双曲线,且该双曲线两焦点间的距离为4,则n的取值范围是
表示双曲线,且该双曲线两焦点间的距离为4,则n的取值范围是| A.(–1,3) | B.(–1, ) ) | C.(0,3) | D.(0, ) ) |
6.如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是 ,则它的表面积是
,则它的表面积是

 ,则它的表面积是
,则它的表面积是
| A.17π | B.18π | C.20π | D.28π |
7.函数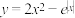 在
在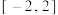 的图象大致为( )
的图象大致为( )
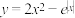 在
在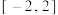 的图象大致为( )
的图象大致为( )A. | B. |
C. | D. |
8.若 ,
, ,则( )
,则( )
 ,
, ,则( )
,则( )A. | B. | C. | D. |
9.执行如图的程序框图,如果输入的 ,则输出
,则输出 的值满足
的值满足
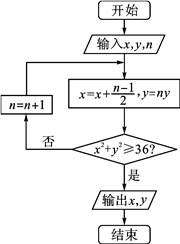
 ,则输出
,则输出 的值满足
的值满足
A. | B. | C. | D. |
10.以抛物线C的顶点为圆心的圆交C于A、B两点,交C的准线于D、E两点.已知|AB|= ,|DE|=
,|DE|= ,则C的焦点到准线的距离为
,则C的焦点到准线的距离为
 ,|DE|=
,|DE|= ,则C的焦点到准线的距离为
,则C的焦点到准线的距离为 | A.8 | B.6 | C.4 | D.2 |
11.平面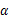 过正方体ABCD—A1B1C1D1的顶点A,
过正方体ABCD—A1B1C1D1的顶点A, ,
, ,
, ,则m,n所成角的正弦值为
,则m,n所成角的正弦值为
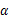 过正方体ABCD—A1B1C1D1的顶点A,
过正方体ABCD—A1B1C1D1的顶点A, ,
, ,
, ,则m,n所成角的正弦值为
,则m,n所成角的正弦值为A. | B. | C. | D. |
12.已知函数 为
为 的零点,
的零点, 为
为 图象的对称轴,且
图象的对称轴,且 在
在 单调,则
单调,则 的最大值为
的最大值为
 为
为 的零点,
的零点, 为
为 图象的对称轴,且
图象的对称轴,且 在
在 单调,则
单调,则 的最大值为
的最大值为| A.11 | B.9 |
| C.7 | D.5 |
13.设向量a=(m,1),b=(1,2),且|a+b|2=|a|2+|b|2,则m=_________.
14. 的展开式中,x3的系数是_________.(用数字填写答案)
的展开式中,x3的系数是_________.(用数字填写答案)
 的展开式中,x3的系数是_________.(用数字填写答案)
的展开式中,x3的系数是_________.(用数字填写答案)15.设等比数列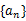 满足a1+a3=10,a2+a4=5,则a1a2…an的最大值为 .
满足a1+a3=10,a2+a4=5,则a1a2…an的最大值为 .
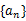 满足a1+a3=10,a2+a4=5,则a1a2…an的最大值为 .
满足a1+a3=10,a2+a4=5,则a1a2…an的最大值为 .16.某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5 kg,乙材料1 kg,用5个工时;生产一件产品B需要甲材料0.5 kg,乙材料0.3 kg,用3个工时,生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150 kg,乙材料90 kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为______元.
17. 的内角A,B,C的对边分别为a,b,c.已知
的内角A,B,C的对边分别为a,b,c.已知 .
.
(1)求角C;(2)若 ,
, ,求
,求 的周长.
的周长.
 的内角A,B,C的对边分别为a,b,c.已知
的内角A,B,C的对边分别为a,b,c.已知 .
.(1)求角C;(2)若
 ,
, ,求
,求 的周长.
的周长.18.如图,在以 ,
, ,
, ,
, ,
, ,
, 为顶点的五面体中,面
为顶点的五面体中,面 为正方形,
为正方形, ,
, ,且二面角
,且二面角 与二面角
与二面角 都是
都是 .
.

(1)证明:平面 平面
平面 ;
;
(2)求二面角 的余弦值.
的余弦值.
 ,
, ,
, ,
, ,
, ,
, 为顶点的五面体中,面
为顶点的五面体中,面 为正方形,
为正方形, ,
, ,且二面角
,且二面角 与二面角
与二面角 都是
都是 .
.
(1)证明:平面
 平面
平面 ;
;(2)求二面角
 的余弦值.
的余弦值.19.某公司计划购买2台机器,该种机器使用三年后即被淘汰,机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:

以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率,记X表示2台机器三年内共需更换的易损零件数,n表示购买2台机器的同时购买的易损零件数.
(1)求X的分布列;
(2)若要求 ,确定n的最小值;
,确定n的最小值;
(3)以购买易损零件所需费用的期望值为决策依据,在 与
与 之中选其一,应选用哪个?
之中选其一,应选用哪个?

以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率,记X表示2台机器三年内共需更换的易损零件数,n表示购买2台机器的同时购买的易损零件数.
(1)求X的分布列;
(2)若要求
 ,确定n的最小值;
,确定n的最小值;(3)以购买易损零件所需费用的期望值为决策依据,在
 与
与 之中选其一,应选用哪个?
之中选其一,应选用哪个?20.设圆 的圆心为A,直线l过点B(1,0)且与x轴不重合,l交圆A于C,D两点,过B作AC的平行线交AD于点E.
的圆心为A,直线l过点B(1,0)且与x轴不重合,l交圆A于C,D两点,过B作AC的平行线交AD于点E.
(I)证明 为定值,并写出点E的轨迹方程;
为定值,并写出点E的轨迹方程;
(II)设点E的轨迹为曲线C1,直线l交C1于M,N两点,过B且与l垂直的直线与圆A交于P,Q两点,求四边形MPNQ面积的取值范围.
 的圆心为A,直线l过点B(1,0)且与x轴不重合,l交圆A于C,D两点,过B作AC的平行线交AD于点E.
的圆心为A,直线l过点B(1,0)且与x轴不重合,l交圆A于C,D两点,过B作AC的平行线交AD于点E.(I)证明
 为定值,并写出点E的轨迹方程;
为定值,并写出点E的轨迹方程;(II)设点E的轨迹为曲线C1,直线l交C1于M,N两点,过B且与l垂直的直线与圆A交于P,Q两点,求四边形MPNQ面积的取值范围.
21.已知函数 有两个零点.
有两个零点.
(Ⅰ)求a的取值范围;
(Ⅱ)设x1,x2是 的两个零点,证明:
的两个零点,证明: .
.
 有两个零点.
有两个零点.(Ⅰ)求a的取值范围;
(Ⅱ)设x1,x2是
 的两个零点,证明:
的两个零点,证明: .
.22.选修4-1:几何证明选讲
如图,△OAB是等腰三角形,∠AOB=120°.以O为圆心, OA为半径作圆.
OA为半径作圆.
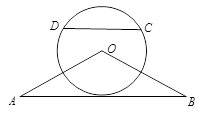
(Ⅰ)证明:直线AB与 相切;
相切;
(Ⅱ)点C,D在⊙O上,且A,B,C,D四点共圆,证明:AB∥CD.
如图,△OAB是等腰三角形,∠AOB=120°.以O为圆心,
 OA为半径作圆.
OA为半径作圆.
(Ⅰ)证明:直线AB与
 相切;
相切;(Ⅱ)点C,D在⊙O上,且A,B,C,D四点共圆,证明:AB∥CD.
23.选修4 4:坐标系与参数方程
4:坐标系与参数方程
在直角坐标系xOy中,曲线C1的参数方程为 (t为参数,a>0).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=4cos θ.
(t为参数,a>0).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=4cos θ.
(Ⅰ)说明C1是哪种曲线,并将C1的方程化为极坐标方程;
(Ⅱ)直线C3的极坐标方程为θ=α0,其中α0满足tan α0=2,若曲线C1与C2的公共点都在C3上,求a.
 4:坐标系与参数方程
4:坐标系与参数方程在直角坐标系xOy中,曲线C1的参数方程为
 (t为参数,a>0).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=4cos θ.
(t为参数,a>0).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=4cos θ.(Ⅰ)说明C1是哪种曲线,并将C1的方程化为极坐标方程;
(Ⅱ)直线C3的极坐标方程为θ=α0,其中α0满足tan α0=2,若曲线C1与C2的公共点都在C3上,求a.
24.选修4 5:不等式选讲
5:不等式选讲
已知函数f(x)= ∣x+1∣ ∣2x
∣2x 3∣.
3∣.
(Ⅰ)在答题卡第(24)题图中画出y= f(x)的图像;
(Ⅱ)求不等式∣f(x)∣﹥1的解集.
 5:不等式选讲
5:不等式选讲已知函数f(x)= ∣x+1∣
 ∣2x
∣2x 3∣.
3∣.(Ⅰ)在答题卡第(24)题图中画出y= f(x)的图像;
(Ⅱ)求不等式∣f(x)∣﹥1的解集.

 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
