全一卷
1.已知 、
、 、
、 都是锐角,用“>”号连接
都是锐角,用“>”号连接 是______.
是______.
 、
、 、
、 都是锐角,用“>”号连接
都是锐角,用“>”号连接 是______.
是______.2.三角方程 在区间
在区间 内的所有解的和是______.
内的所有解的和是______.
 在区间
在区间 内的所有解的和是______.
内的所有解的和是______.3.已知满足条件 的复数
的复数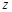 在复平面内所对应的点的集合是一条二次曲线,则该二次曲线的离心率
在复平面内所对应的点的集合是一条二次曲线,则该二次曲线的离心率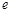 ______.
______.
 的复数
的复数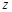 在复平面内所对应的点的集合是一条二次曲线,则该二次曲线的离心率
在复平面内所对应的点的集合是一条二次曲线,则该二次曲线的离心率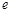 ______.
______.4.已知直角 斜边上的高是
斜边上的高是 ,且
,且 .将
.将 绕
绕 旋转至
旋转至 ,使二面角
,使二面角 为
为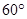 .则异面直线
.则异面直线 与
与 所成角的大小是______(用反三角函数表示).
所成角的大小是______(用反三角函数表示).
 斜边上的高是
斜边上的高是 ,且
,且 .将
.将 绕
绕 旋转至
旋转至 ,使二面角
,使二面角 为
为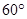 .则异面直线
.则异面直线 与
与 所成角的大小是______(用反三角函数表示).
所成角的大小是______(用反三角函数表示).5.若关于 的二次方程
的二次方程 至少有一个整数根,则正整数
至少有一个整数根,则正整数 的值是__________.
的值是__________.
 的二次方程
的二次方程 至少有一个整数根,则正整数
至少有一个整数根,则正整数 的值是__________.
的值是__________.6.从集合 中选取四个各不相等的数,使它们按从小到大的顺序组成公比为整数的等比数列.则这样的等比数列共有______个.
中选取四个各不相等的数,使它们按从小到大的顺序组成公比为整数的等比数列.则这样的等比数列共有______个.
 中选取四个各不相等的数,使它们按从小到大的顺序组成公比为整数的等比数列.则这样的等比数列共有______个.
中选取四个各不相等的数,使它们按从小到大的顺序组成公比为整数的等比数列.则这样的等比数列共有______个.7.连接椭圆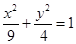 的右焦点
的右焦点 与椭圆上动点
与椭圆上动点 ,作正方形
,作正方形 (
( 、
、 、
、 、
、 四点按顺时针方向排列).则当点
四点按顺时针方向排列).则当点 沿椭圆运动一周后,动点
沿椭圆运动一周后,动点 的轨迹方程是
的轨迹方程是______ .
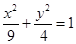 的右焦点
的右焦点 与椭圆上动点
与椭圆上动点 ,作正方形
,作正方形 (
( 、
、 、
、 、
、 四点按顺时针方向排列).则当点
四点按顺时针方向排列).则当点 沿椭圆运动一周后,动点
沿椭圆运动一周后,动点 的轨迹方程是
的轨迹方程是8.四个半径都是1的球两两外切,都在一个大球里面,且都与大球相切.则这个大球的半径是______.
9.点集 所构成的平面图形的面积是______.
所构成的平面图形的面积是______.
 所构成的平面图形的面积是______.
所构成的平面图形的面积是______.10.若关于 的不等式
的不等式 仅有负数解,则实数
仅有负数解,则实数 的取值范围是______.
的取值范围是______.
 的不等式
的不等式 仅有负数解,则实数
仅有负数解,则实数 的取值范围是______.
的取值范围是______.11.设 是正整数,且没有两个是相邻的,又对于
是正整数,且没有两个是相邻的,又对于 .求证:对每一个正整数
.求证:对每一个正整数 ,区间
,区间 中至少含有一个完全平方数.
中至少含有一个完全平方数.
 是正整数,且没有两个是相邻的,又对于
是正整数,且没有两个是相邻的,又对于 .求证:对每一个正整数
.求证:对每一个正整数 ,区间
,区间 中至少含有一个完全平方数.
中至少含有一个完全平方数.12.已知集合 .求该集合具有下列性质的子集个数:每个子集至少含有
.求该集合具有下列性质的子集个数:每个子集至少含有 个元素,且每个子集中任意两个元素的差的绝对值大于1.
个元素,且每个子集中任意两个元素的差的绝对值大于1.
 .求该集合具有下列性质的子集个数:每个子集至少含有
.求该集合具有下列性质的子集个数:每个子集至少含有 个元素,且每个子集中任意两个元素的差的绝对值大于1.
个元素,且每个子集中任意两个元素的差的绝对值大于1.13.平面上给定 个点
个点 ,任意三点不共线.由其中
,任意三点不共线.由其中 个点对确定
个点对确定 条直线(即过
条直线(即过 个点对中的每一点对作一条直线),使这
个点对中的每一点对作一条直线),使这 条直线不相交成三个顶点都是给定点的三角形.求
条直线不相交成三个顶点都是给定点的三角形.求 的最大值.
的最大值.
 个点
个点 ,任意三点不共线.由其中
,任意三点不共线.由其中 个点对确定
个点对确定 条直线(即过
条直线(即过 个点对中的每一点对作一条直线),使这
个点对中的每一点对作一条直线),使这 条直线不相交成三个顶点都是给定点的三角形.求
条直线不相交成三个顶点都是给定点的三角形.求 的最大值.
的最大值. 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
