全一卷
1.若集合 ,则
,则 等于( )
等于( )
 ,则
,则 等于( )
等于( )A. | B. | C. | D.R |
2.下列函数中,与函数 有相同定义域的是
有相同定义域的是
 有相同定义域的是
有相同定义域的是A. | B. | C. | D. |
3.一个容量100的样本,其数据的分组与各组的频数如下表
则样本数据落在 上的频率为
上的频率为
| 组别 |  |  |  |  |  |  |  |
| 频数 | 12 | 13 | 24 | 15 | 16 | 13 | 7 |
则样本数据落在
 上的频率为
上的频率为| A.0.13 | B.0.39 | C.0.52 | D.0.64 |
4.若双曲线 的离心率为2,则
的离心率为2,则 等于( )
等于( )
 的离心率为2,则
的离心率为2,则 等于( )
等于( )| A.2 | B. | C.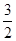 | D.1 |
5.如图,某几何体的正视图与侧视图都是边长为1的正方形,且体积为 .则该几何体的俯视图可以是( )
.则该几何体的俯视图可以是( )

 .则该几何体的俯视图可以是( )
.则该几何体的俯视图可以是( )
A. | B. | C. | D. |
6.阅读下图所示的程序框图,运行相应的程序,输出的结果是()


| A.-1 | B.2 | C.3 | D.4 |
7.已知锐角△ABC的面积为 ,BC=4,CA=3,则角C的大小为
,BC=4,CA=3,则角C的大小为
 ,BC=4,CA=3,则角C的大小为
,BC=4,CA=3,则角C的大小为| A.75° | B.60° | C.45° | D.30° |
8.定义在R上的偶函数 的部分图像如右图所示,则在
的部分图像如右图所示,则在 上,下列函数中与
上,下列函数中与 的单调性不同的是( )
的单调性不同的是( )

 的部分图像如右图所示,则在
的部分图像如右图所示,则在 上,下列函数中与
上,下列函数中与 的单调性不同的是( )
的单调性不同的是( )
A. |
B. |
C. |
D. |
9.在平面直角坐标系中,若不等式组 (
( 为常数)所表示的平面区域内的面积等于2,则
为常数)所表示的平面区域内的面积等于2,则 的值为
的值为
 (
( 为常数)所表示的平面区域内的面积等于2,则
为常数)所表示的平面区域内的面积等于2,则 的值为
的值为| A.-5 | B.1 | C.2 | D.3 |
10.设 是平面
是平面 内的两条不同直线;
内的两条不同直线; 是平面
是平面 内的两条相交直线,则
内的两条相交直线,则 的一个充分而不必要条件是( )
的一个充分而不必要条件是( )
 是平面
是平面 内的两条不同直线;
内的两条不同直线; 是平面
是平面 内的两条相交直线,则
内的两条相交直线,则 的一个充分而不必要条件是( )
的一个充分而不必要条件是( )A. | B. | C. | D. |
11.若函数 的零点与
的零点与  的零点之差的绝对值不超过0.25, 则
的零点之差的绝对值不超过0.25, 则 可以是
可以是
 的零点与
的零点与  的零点之差的绝对值不超过0.25, 则
的零点之差的绝对值不超过0.25, 则 可以是
可以是A. | B. |
C. | D. |
12.设 ,
, ,
, 为同一平面内具有相同起点的任意三个非零向量,且满足
为同一平面内具有相同起点的任意三个非零向量,且满足 与
与 不共线,
不共线,

 ,∣
,∣ ∣=∣
∣=∣ ∣,则∣
∣,则∣ •
• ∣的值一定等于( )
∣的值一定等于( )
 ,
, ,
, 为同一平面内具有相同起点的任意三个非零向量,且满足
为同一平面内具有相同起点的任意三个非零向量,且满足 与
与 不共线,
不共线,

 ,∣
,∣ ∣=∣
∣=∣ ∣,则∣
∣,则∣ •
• ∣的值一定等于( )
∣的值一定等于( )A.以 , , 为邻边的平行四边形的面积 为邻边的平行四边形的面积 | B.以 , , 为两边的三角形面积 为两边的三角形面积 |
C. , , 为两边的三角形面积 为两边的三角形面积 | D.以 , , 为邻边的平行四边形的面积 为邻边的平行四边形的面积 |
13.复数 的实部是 .
的实部是 .
 的实部是 .
的实部是 .14.点A为周长等于3的圆周上的一个定点,若在该圆周上随机取一点B,则劣弧 AB的长度小于1的概率为 .
AB的长度小于1的概率为 .
 AB的长度小于1的概率为 .
AB的长度小于1的概率为 .15.若曲线 存在垂直于
存在垂直于 轴的切线,则实数
轴的切线,则实数 的取值范围是
的取值范围是_________
 存在垂直于
存在垂直于 轴的切线,则实数
轴的切线,则实数 的取值范围是
的取值范围是16.五位同学围成一圈依序循环报数,规定:
①第一位同学首次报出的数为1.第二位同学首次报出的数也为1,之后每位同学所报出的数都是前两位同学所报出的数之和;
②若报出的是为3的倍数,则报该数的同学需拍手一次,
当第30个数被报出时,五位同学拍手的总次数为 .
①第一位同学首次报出的数为1.第二位同学首次报出的数也为1,之后每位同学所报出的数都是前两位同学所报出的数之和;
②若报出的是为3的倍数,则报该数的同学需拍手一次,
当第30个数被报出时,五位同学拍手的总次数为 .
17.等比数列 中,已知
中,已知 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若 分别为等差数列
分别为等差数列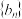 的第3项和第5项,试求数列
的第3项和第5项,试求数列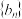 的通项公式及前
的通项公式及前 项和
项和 .
.
 中,已知
中,已知 .
.(1)求数列
 的通项公式;
的通项公式; (2)若
 分别为等差数列
分别为等差数列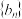 的第3项和第5项,试求数列
的第3项和第5项,试求数列 的通项公式及前
的通项公式及前 项和
项和 .
.18.袋中有大小、形状相同的红、黑球各一个,现一次有放回地随机摸取3次,每次摸取一个球
(I)试问:一共有多少种不同的结果?请列出所有可能的结果;
(Ⅱ)若摸到红球时得2分,摸到黑球时得1分,求3次摸球所得总分为5的概率.
(I)试问:一共有多少种不同的结果?请列出所有可能的结果;
(Ⅱ)若摸到红球时得2分,摸到黑球时得1分,求3次摸球所得总分为5的概率.
19.已知函数 其中
其中 ,
, ,
,
(1)若 求
求 的值;
的值;
(2)在(1)的条件下,若函数 的图象的相邻两条对称轴之间的距离等于
的图象的相邻两条对称轴之间的距离等于 ,求函数
,求函数 的解析式;并求最小正实数
的解析式;并求最小正实数 ,使得函数
,使得函数 的图象向左平移
的图象向左平移 个单位所对应的函数是偶函数.
个单位所对应的函数是偶函数.
 其中
其中 ,
, ,
,(1)若
 求
求 的值;
的值;(2)在(1)的条件下,若函数
 的图象的相邻两条对称轴之间的距离等于
的图象的相邻两条对称轴之间的距离等于 ,求函数
,求函数 的解析式;并求最小正实数
的解析式;并求最小正实数 ,使得函数
,使得函数 的图象向左平移
的图象向左平移 个单位所对应的函数是偶函数.
个单位所对应的函数是偶函数.20.
如图,平行四边形 中,
中, ,
, 将
将 沿
沿 折起到
折起到 的位置,使平面
的位置,使平面 平面
平面 .
.
(Ⅰ)求证: ;
;
(Ⅱ)求三棱锥 的侧面积.
的侧面积.
如图,平行四边形
 中,
中, ,
, 将
将 沿
沿 折起到
折起到 的位置,使平面
的位置,使平面 平面
平面 .
.(Ⅰ)求证:
 ;
;(Ⅱ)求三棱锥
 的侧面积.
的侧面积.
21.
已知函数 ,且
,且 .
.
(I)试用含 的代数式表示
的代数式表示 ;
;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)令 ,设函数
,设函数 在
在 处取得极值,记点
处取得极值,记点 ,证明:线段
,证明:线段 与曲线
与曲线 存在异于
存在异于 、
、 的公共点.
的公共点.
已知函数
 ,且
,且 .
.(I)试用含
 的代数式表示
的代数式表示 ;
;(Ⅱ)求
 的单调区间;
的单调区间;(Ⅲ)令
 ,设函数
,设函数 在
在 处取得极值,记点
处取得极值,记点 ,证明:线段
,证明:线段 与曲线
与曲线 存在异于
存在异于 、
、 的公共点.
的公共点. 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
