全一卷
1.已知集合 ,
, ,若
,若 则实数
则实数 的值为
的值为________
 ,
, ,若
,若 则实数
则实数 的值为
的值为2.已知复数z=(1+i)(1+2i),其中i是虚数单位,则z的模是__________
3.某工厂生产甲、乙、丙、丁四种不同型号的产品,产量分别为200,400,300,100件,为检验产品的质量,现用分层抽样的方法从以上所有的产品中抽取60件进行检验,则应从丙种型号的产品中抽取________ 件.
4.
如图是一个算法流程图,若输入x的值为 ,则输出y的值是____.
,则输出y的值是____.

5.若 ,则
,则
____________ .
 ,则
,则
6.如图,在圆柱O1 O2 内有一个球O,该球与圆柱的上、下底面及母线均相切.记圆柱O1 O2 的体积为V1 ,球O的体积为V2 ,则 的值是
的值是_____

 的值是
的值是
7.记函数 的定义域为
的定义域为 ,在区间
,在区间 上随机取一个数
上随机取一个数 ,则
,则 的概率是
的概率是________ .
 的定义域为
的定义域为 ,在区间
,在区间 上随机取一个数
上随机取一个数 ,则
,则 的概率是
的概率是8.在平面直角坐标系xOy中,双曲线 的右准线与它的两条渐近线分别交于点
的右准线与它的两条渐近线分别交于点
P,Q,其焦点是F1 ,F2 ,则四边形F1 P F2 Q的面积是________ .
 的右准线与它的两条渐近线分别交于点
的右准线与它的两条渐近线分别交于点P,Q,其焦点是F1 ,F2 ,则四边形F1 P F2 Q的面积是
9.等比数列{ }的各项均为实数,其前
}的各项均为实数,其前 项为
项为 ,已知
,已知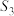 =
= ,
, =
= ,则
,则 =
=_____ .
 }的各项均为实数,其前
}的各项均为实数,其前 项为
项为 ,已知
,已知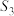 =
= ,
, =
= ,则
,则 =
=10.某公司一年购买某种货物 吨,每次购买
吨,每次购买 吨,运费为
吨,运费为 万元/次,一年的总存储费用为
万元/次,一年的总存储费用为 万元.要使一年的总运费与总存储费用之和最小,则
万元.要使一年的总运费与总存储费用之和最小,则 的值是
的值是__________ .
 吨,每次购买
吨,每次购买 吨,运费为
吨,运费为 万元/次,一年的总存储费用为
万元/次,一年的总存储费用为 万元.要使一年的总运费与总存储费用之和最小,则
万元.要使一年的总运费与总存储费用之和最小,则 的值是
的值是11.已知函数 ,其中e是自然数对数的底数,若
,其中e是自然数对数的底数,若 ,则实数a的取值范围是
,则实数a的取值范围是_________ .
 ,其中e是自然数对数的底数,若
,其中e是自然数对数的底数,若 ,则实数a的取值范围是
,则实数a的取值范围是12.在同一个平面内,向量 的模分别为
的模分别为 与
与 的夹角为
的夹角为 ,且
,且 与
与 的夹角为
的夹角为 ,若
,若 ,则
,则
_________ .

 的模分别为
的模分别为 与
与 的夹角为
的夹角为 ,且
,且 与
与 的夹角为
的夹角为 ,若
,若 ,则
,则

13.在平面直角坐标系xOy中,A(-12,0),B(0,6),点P在圆O:x2+y2=50上,若 ·
·
 20,则点P的横坐标的取值范围是
20,则点P的横坐标的取值范围是_________
 ·
·
 20,则点P的横坐标的取值范围是
20,则点P的横坐标的取值范围是14.设 是定义在R 且周期为1的函数,在区间
是定义在R 且周期为1的函数,在区间 上,
上, 其中集合
其中集合 ,则方程
,则方程 的解的个数是
的解的个数是____________
 是定义在R 且周期为1的函数,在区间
是定义在R 且周期为1的函数,在区间 上,
上, 其中集合
其中集合 ,则方程
,则方程 的解的个数是
的解的个数是15.如图,在三棱锥ABCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E,F(E与A,D不重合)分别在棱AD,BD上,且EF⊥AD.
求证:(1)EF∥平面ABC;
(2)AD⊥AC.

求证:(1)EF∥平面ABC;
(2)AD⊥AC.
16.已知向量 .
.
(1)若 ,求x的值;
,求x的值;
(2)记 ,求函数y=f(x)的最大值和最小值及对应的x的值.
,求函数y=f(x)的最大值和最小值及对应的x的值.
 .
.(1)若
 ,求x的值;
,求x的值;(2)记
 ,求函数y=f(x)的最大值和最小值及对应的x的值.
,求函数y=f(x)的最大值和最小值及对应的x的值.17.如图,在平面直角坐标系xOy中,椭圆 的左、右焦点分别为F1,F2,离心率为
的左、右焦点分别为F1,F2,离心率为 ,两准线之间的距离为8.点P在椭圆E上,且位于第一象限,过点F1作直线PF1的垂线l1,过点F2作直线PF2的垂线l2.
,两准线之间的距离为8.点P在椭圆E上,且位于第一象限,过点F1作直线PF1的垂线l1,过点F2作直线PF2的垂线l2.

(1)求椭圆E的标准方程;
(2)若直线l1,l2的交点Q在椭圆E上,求点P的坐标.
 的左、右焦点分别为F1,F2,离心率为
的左、右焦点分别为F1,F2,离心率为 ,两准线之间的距离为8.点P在椭圆E上,且位于第一象限,过点F1作直线PF1的垂线l1,过点F2作直线PF2的垂线l2.
,两准线之间的距离为8.点P在椭圆E上,且位于第一象限,过点F1作直线PF1的垂线l1,过点F2作直线PF2的垂线l2.
(1)求椭圆E的标准方程;
(2)若直线l1,l2的交点Q在椭圆E上,求点P的坐标.
18.如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm,容器Ⅰ的底面对角线AC的长为10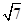 cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm. 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm. 现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm. 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm. 现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
(1)将l放在容器Ⅰ中,l的一端置于点A处,另一端置于侧棱CC1上,求l没入水中部分的长度;
(2)将l放在容器Ⅱ中,l的一端置于点E处,另一端置于侧棱GG1上,求l没入水中部分的长度.

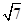 cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm. 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm. 现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm. 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm. 现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)(1)将l放在容器Ⅰ中,l的一端置于点A处,另一端置于侧棱CC1上,求l没入水中部分的长度;
(2)将l放在容器Ⅱ中,l的一端置于点E处,另一端置于侧棱GG1上,求l没入水中部分的长度.

19.对于给定的正整数k,若数列{an}满足
对任意正整数n(n> k) 总成立,则称数列{an} 是“P(k)数列”.
(1)证明:等差数列{an}是“P(3)数列”;
(2)若数列{an}既是“P(2)数列”,又是“P(3)数列”,证明:{an}是等差数列.

对任意正整数n(n> k) 总成立,则称数列{an} 是“P(k)数列”.
(1)证明:等差数列{an}是“P(3)数列”;
(2)若数列{an}既是“P(2)数列”,又是“P(3)数列”,证明:{an}是等差数列.
20.已知函数 有极值,且导函数
有极值,且导函数 的极值点是
的极值点是 的零点.(极值点是指函数取极值时对应的自变量的值)
的零点.(极值点是指函数取极值时对应的自变量的值)
(1)求b关于a的函数关系式,并写出定义域;
(2)证明:b²>3a;
(3)若 ,
, 这两个函数的所有极值之和不小于
这两个函数的所有极值之和不小于 ,求a的取值范围.
,求a的取值范围.
 有极值,且导函数
有极值,且导函数 的极值点是
的极值点是 的零点.(极值点是指函数取极值时对应的自变量的值)
的零点.(极值点是指函数取极值时对应的自变量的值)(1)求b关于a的函数关系式,并写出定义域;
(2)证明:b²>3a;
(3)若
 ,
, 这两个函数的所有极值之和不小于
这两个函数的所有极值之和不小于 ,求a的取值范围.
,求a的取值范围.21.(选修4-1:几何证明选讲)
如图,AB为半圆O的直径,直线PC切半圆O于点C,AP⊥PC,P为垂足。

求证:(1)∠PAC=∠CAB;
(2)AC2 =AP·AB
如图,AB为半圆O的直径,直线PC切半圆O于点C,AP⊥PC,P为垂足。

求证:(1)∠PAC=∠CAB;
(2)AC2 =AP·AB
22.[选修4-2:矩阵与变换]已知矩阵A= ,B=
,B= .
.
求AB;
若曲线C1; 在矩阵AB对应的变换作用下得到另一曲线C2 ,求C2的方程.
在矩阵AB对应的变换作用下得到另一曲线C2 ,求C2的方程.
 ,B=
,B= .
.求AB;
若曲线C1;
 在矩阵AB对应的变换作用下得到另一曲线C2 ,求C2的方程.
在矩阵AB对应的变换作用下得到另一曲线C2 ,求C2的方程.23.已知直线l的参数方程为 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 (s为参数).设p为曲线C上的动点,求点P到直线l的距离的最小值
(s为参数).设p为曲线C上的动点,求点P到直线l的距离的最小值
 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 (s为参数).设p为曲线C上的动点,求点P到直线l的距离的最小值
(s为参数).设p为曲线C上的动点,求点P到直线l的距离的最小值24.已知a,b,c,d为实数,且a2+b2=4,c2+d2=16,证明ac+bd 8.
8.
 8.
8.25.如图,在平行六面体ABCD-A1B1C1D1中,AA1⊥平面ABCD,且AB=AD=2,AA1= ,∠BAD=120°.
,∠BAD=120°.

(1)求异面直线A1B与AC1所成角的余弦值;
(2)求二面角B-A1D-A的正弦值.
 ,∠BAD=120°.
,∠BAD=120°.
(1)求异面直线A1B与AC1所成角的余弦值;
(2)求二面角B-A1D-A的正弦值.
26.已知一个口袋有m个白球,n个黑球(m,n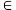
 ,n
,n 2),这些球除颜色外全部相同.现将口袋中的球随机的逐个取出,并放入如图所示的编号为1,2,3,……,m+n的抽屉内,其中第k次取球放入编号为k的抽屉(k=1,2,3,……,m+n).
2),这些球除颜色外全部相同.现将口袋中的球随机的逐个取出,并放入如图所示的编号为1,2,3,……,m+n的抽屉内,其中第k次取球放入编号为k的抽屉(k=1,2,3,……,m+n).

(1)试求编号为2的抽屉内放的是黑球的概率p;
(2)随机变量x表示最后一个取出的黑球所在抽屉编号的倒数,E(x)是x的数学期望,证明
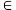
 ,n
,n 2),这些球除颜色外全部相同.现将口袋中的球随机的逐个取出,并放入如图所示的编号为1,2,3,……,m+n的抽屉内,其中第k次取球放入编号为k的抽屉(k=1,2,3,……,m+n).
2),这些球除颜色外全部相同.现将口袋中的球随机的逐个取出,并放入如图所示的编号为1,2,3,……,m+n的抽屉内,其中第k次取球放入编号为k的抽屉(k=1,2,3,……,m+n).
(1)试求编号为2的抽屉内放的是黑球的概率p;
(2)随机变量x表示最后一个取出的黑球所在抽屉编号的倒数,E(x)是x的数学期望,证明

 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
