全一卷
1.已知集合 ,集合
,集合 ,则
,则
_______ .
 ,集合
,集合 ,则
,则
2.若排列数 ,则
,则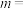
________
 ,则
,则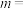
3.不等式 的解集为
的解集为________
 的解集为
的解集为4.已知球的体积为 ,则该球主视图的面积等于
,则该球主视图的面积等于________
 ,则该球主视图的面积等于
,则该球主视图的面积等于5.已知复数 满足
满足 ,则
,则
_____________ .
 满足
满足 ,则
,则
6.设双曲线
 的焦点为
的焦点为 、
、 ,
, 为该双曲线上的一点,若
为该双曲线上的一点,若 ,则
,则
________

 的焦点为
的焦点为 、
、 ,
, 为该双曲线上的一点,若
为该双曲线上的一点,若 ,则
,则
7.如图,以长方体 的顶点
的顶点 为坐标原点,过
为坐标原点,过 的三条棱所在的直线为坐标轴,建立空间直角坐标系,若
的三条棱所在的直线为坐标轴,建立空间直角坐标系,若 的坐标为
的坐标为 ,则
,则 的坐标为
的坐标为________

 的顶点
的顶点 为坐标原点,过
为坐标原点,过 的三条棱所在的直线为坐标轴,建立空间直角坐标系,若
的三条棱所在的直线为坐标轴,建立空间直角坐标系,若 的坐标为
的坐标为 ,则
,则 的坐标为
的坐标为
8.定义在 上的函数
上的函数 的反函数为
的反函数为 ,若
,若 为奇函数,则
为奇函数,则 的解为
的解为________ .
 上的函数
上的函数 的反函数为
的反函数为 ,若
,若 为奇函数,则
为奇函数,则 的解为
的解为9.已知四个函数:①  ;②
;②  ;③
;③  ;④
;④  . 从中任选2个,则事件“所选2个函数的图像有且仅有一个公共点”的概率为
. 从中任选2个,则事件“所选2个函数的图像有且仅有一个公共点”的概率为________
 ;②
;②  ;③
;③  ;④
;④  . 从中任选2个,则事件“所选2个函数的图像有且仅有一个公共点”的概率为
. 从中任选2个,则事件“所选2个函数的图像有且仅有一个公共点”的概率为10.已知数列 和
和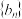 ,其中
,其中 ,
, ,
,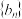 的项是互不相等的正整数,若对于任意
的项是互不相等的正整数,若对于任意 ,
,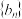 的第
的第 项等于
项等于 的第
的第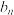 项,则
项,则
________
 和
和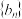 ,其中
,其中 ,
, ,
,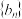 的项是互不相等的正整数,若对于任意
的项是互不相等的正整数,若对于任意 ,
,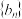 的第
的第 项等于
项等于 的第
的第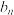 项,则
项,则
11.设 、
、 ,且
,且 ,则
,则 的最小值等于
的最小值等于________
 、
、 ,且
,且 ,则
,则 的最小值等于
的最小值等于12.如图,用35个单位正方形拼成一个矩形,点 、
、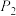 、
、 、
、 以及四个标记为“”的点在正方形的顶点处,设集合
以及四个标记为“”的点在正方形的顶点处,设集合 ,点
,点 ,过
,过 作直线
作直线 ,使得不在
,使得不在 上的“”的点分布在
上的“”的点分布在 的两侧. 用
的两侧. 用 和
和 分别表示
分别表示 一侧和另一侧的“”的点到
一侧和另一侧的“”的点到 的距离之和. 若过
的距离之和. 若过 的直线
的直线 中有且只有一条满足
中有且只有一条满足 ,则
,则 中所有这样的
中所有这样的 为
为________

 、
、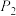 、
、 、
、 以及四个标记为“”的点在正方形的顶点处,设集合
以及四个标记为“”的点在正方形的顶点处,设集合 ,点
,点 ,过
,过 作直线
作直线 ,使得不在
,使得不在 上的“”的点分布在
上的“”的点分布在 的两侧. 用
的两侧. 用 和
和 分别表示
分别表示 一侧和另一侧的“”的点到
一侧和另一侧的“”的点到 的距离之和. 若过
的距离之和. 若过 的直线
的直线 中有且只有一条满足
中有且只有一条满足 ,则
,则 中所有这样的
中所有这样的 为
为
13.关于 、
、 的二元一次方程组
的二元一次方程组 的系数行列式
的系数行列式 为( )
为( )
 、
、 的二元一次方程组
的二元一次方程组 的系数行列式
的系数行列式 为( )
为( )A. | B. | C. | D. |
14.在数列 中,
中, ,
, ,则
,则 ( )
( )
 中,
中, ,
, ,则
,则 ( )
( )A.等于 | B.等于0 | C.等于 | D.不存在 |
15.已知 、
、 、
、 为实常数,数列
为实常数,数列 的通项
的通项 ,
, ,则“存在
,则“存在 ,
,
使得 、
、 、
、 成等差数列”的一个必要条件是( )
成等差数列”的一个必要条件是( )
 、
、 、
、 为实常数,数列
为实常数,数列 的通项
的通项 ,
, ,则“存在
,则“存在 ,
,使得
 、
、 、
、 成等差数列”的一个必要条件是( )
成等差数列”的一个必要条件是( )A. | B. | C. | D. |
16.在平面直角坐标系 中,已知椭圆
中,已知椭圆 和
和 .
.  为
为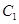 上的动
上的动
点, 为
为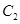 上的动点,
上的动点, 是
是 的最大值. 记
的最大值. 记 在
在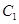 上,
上, 在
在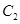 上,且
上,且 ,则
,则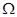 中元素个数为( )
中元素个数为( )
 中,已知椭圆
中,已知椭圆 和
和 .
.  为
为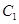 上的动
上的动点,
 为
为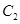 上的动点,
上的动点, 是
是 的最大值. 记
的最大值. 记 在
在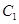 上,
上, 在
在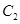 上,且
上,且 ,则
,则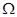 中元素个数为( )
中元素个数为( )| A.2个 | B.4个 | C.8个 | D.无穷个 |
17.如图,直三棱柱 的底面为直角三角形,两直角边AB和AC的长分别为4和2,侧棱
的底面为直角三角形,两直角边AB和AC的长分别为4和2,侧棱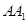 的长为5.
的长为5.
(1)求三棱柱 的体积;
的体积;
(2)设M是BC中点,求直线 与平面
与平面 所成角的大小.
所成角的大小.

 的底面为直角三角形,两直角边AB和AC的长分别为4和2,侧棱
的底面为直角三角形,两直角边AB和AC的长分别为4和2,侧棱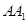 的长为5.
的长为5. (1)求三棱柱
 的体积;
的体积;(2)设M是BC中点,求直线
 与平面
与平面 所成角的大小.
所成角的大小. 
18.已知函数 .
.
(1)求 的单调递增区间;
的单调递增区间;
(2)设 为锐角三角形,角
为锐角三角形,角 所对边
所对边 ,角
,角 所对边
所对边 ,若
,若 ,求
,求 的面积.
的面积.
 .
.(1)求
 的单调递增区间;
的单调递增区间;(2)设
 为锐角三角形,角
为锐角三角形,角 所对边
所对边 ,角
,角 所对边
所对边 ,若
,若 ,求
,求 的面积.
的面积.19.根据预测,某地第
 个月共享单车的投放量和损失量分别为
个月共享单车的投放量和损失量分别为 和
和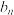 (单位:辆),
(单位:辆),
其中 ,
, ,第
,第 个月底的共享单车的保有量是前
个月底的共享单车的保有量是前 个月的
个月的
累计投放量与累计损失量的差.
(1)求该地区第4个月底的共享单车的保有量;
(2)已知该地共享单车停放点第 个月底的单车容纳量
个月底的单车容纳量 (单位:辆). 设在某月底,共享单车保有量达到最大,问该保有量是否超出了此时停放点的单车容纳量?
(单位:辆). 设在某月底,共享单车保有量达到最大,问该保有量是否超出了此时停放点的单车容纳量?

 个月共享单车的投放量和损失量分别为
个月共享单车的投放量和损失量分别为 和
和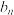 (单位:辆),
(单位:辆),其中
 ,
, ,第
,第 个月底的共享单车的保有量是前
个月底的共享单车的保有量是前 个月的
个月的累计投放量与累计损失量的差.
(1)求该地区第4个月底的共享单车的保有量;
(2)已知该地共享单车停放点第
 个月底的单车容纳量
个月底的单车容纳量 (单位:辆). 设在某月底,共享单车保有量达到最大,问该保有量是否超出了此时停放点的单车容纳量?
(单位:辆). 设在某月底,共享单车保有量达到最大,问该保有量是否超出了此时停放点的单车容纳量?20.在平面直角坐标系xOy中,已知椭圆 ,
, 为
为 的上顶点,
的上顶点, 为
为 上异于
上异于
上、下顶点的动点, 为x正半轴上的动点.
为x正半轴上的动点.
(1)若 在第一象限,且
在第一象限,且 ,求
,求 的坐标;
的坐标;
(2)设 ,若以A、P、M为顶点的三角形是直角三角形,求M的横坐标;
,若以A、P、M为顶点的三角形是直角三角形,求M的横坐标;
(3)若 ,直线AQ与
,直线AQ与 交于另一点C,且
交于另一点C,且 ,
, ,
,
求直线 的方程.
的方程.
 ,
, 为
为 的上顶点,
的上顶点, 为
为 上异于
上异于上、下顶点的动点,
 为x正半轴上的动点.
为x正半轴上的动点.(1)若
 在第一象限,且
在第一象限,且 ,求
,求 的坐标;
的坐标;(2)设
 ,若以A、P、M为顶点的三角形是直角三角形,求M的横坐标;
,若以A、P、M为顶点的三角形是直角三角形,求M的横坐标;(3)若
 ,直线AQ与
,直线AQ与 交于另一点C,且
交于另一点C,且 ,
, ,
,求直线
 的方程.
的方程.21.设定义在 上的函数
上的函数 满足:对于任意的
满足:对于任意的 、
、 ,当
,当 时,都有
时,都有 .
.
(1)若 ,求
,求 的取值范围;
的取值范围;
(2)若 为周期函数,证明:
为周期函数,证明: 是常值函数;
是常值函数;
(3)设 恒大于零,
恒大于零,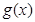 是定义在
是定义在 上、恒大于零的周期函数,
上、恒大于零的周期函数, 是
是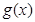 的最大值.
的最大值.
函数 . 证明:“
. 证明:“ 是周期函数”的充要条件是“
是周期函数”的充要条件是“ 是常值函数”.
是常值函数”.
 上的函数
上的函数 满足:对于任意的
满足:对于任意的 、
、 ,当
,当 时,都有
时,都有 .
. (1)若
 ,求
,求 的取值范围;
的取值范围;(2)若
 为周期函数,证明:
为周期函数,证明: 是常值函数;
是常值函数;(3)设
 恒大于零,
恒大于零,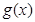 是定义在
是定义在 上、恒大于零的周期函数,
上、恒大于零的周期函数, 是
是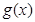 的最大值.
的最大值. 函数
 . 证明:“
. 证明:“ 是周期函数”的充要条件是“
是周期函数”的充要条件是“ 是常值函数”.
是常值函数”. 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
