全一卷
1.若集合 (
(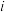 是虚数单位),
是虚数单位), ,则
,则 等于 ( )
等于 ( )
 (
(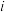 是虚数单位),
是虚数单位), ,则
,则 等于 ( )
等于 ( )A. | B. | C. | D. |
2.下列函数为奇函数的是
A. | B. | C. | D. |
3.若双曲线 的左、右焦点分别为
的左、右焦点分别为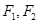 ,点
,点 在双曲线
在双曲线 上,且
上,且 ,则
,则 等于
等于
 的左、右焦点分别为
的左、右焦点分别为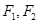 ,点
,点 在双曲线
在双曲线 上,且
上,且 ,则
,则 等于
等于| A.11 | B.9 | C.5 | D.3 |
4.为了解某社区居民的家庭年收入所年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:
根据上表可得回归直线方程 ,其中
,其中 ,据此估计,该社区一户收入为15万元家庭年支出为( )
,据此估计,该社区一户收入为15万元家庭年支出为( )
收入 (万元) (万元) | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
支出 (万元) (万元) | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
根据上表可得回归直线方程
 ,其中
,其中 ,据此估计,该社区一户收入为15万元家庭年支出为( )
,据此估计,该社区一户收入为15万元家庭年支出为( )| A.11.4万元 | B.11.8万元 | C.12.0万元 | D.12.2万元 |
5.若变量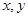 满足约束条件
满足约束条件 则
则 的最小值等于
的最小值等于
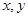 满足约束条件
满足约束条件 则
则 的最小值等于
的最小值等于A. | B.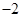 | C. | D.2 |
6.阅读如图所示的程序框图,运行相应的程序,则输出的结果为()


| A.2 | B.1 | C.0 | D.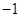 |
7.若 是两条不同的直线,
是两条不同的直线, 垂直于平面
垂直于平面 ,则“
,则“ ”是“
”是“ ”的
”的
 是两条不同的直线,
是两条不同的直线, 垂直于平面
垂直于平面 ,则“
,则“ ”是“
”是“ ”的
”的| A.充分而不必要条件 | B.必要而不充分条件 | C.充分必要条件 | D.既不充分也不必要条件 |
8.若 是函数
是函数 的两个不同的零点,且
的两个不同的零点,且 这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则
这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则 的值等于
的值等于
 是函数
是函数 的两个不同的零点,且
的两个不同的零点,且 这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则
这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则 的值等于
的值等于| A.6 | B.7 | C.8 | D.9 |
9.已知 ,
, ,
, ,若
,若 点是
点是 所在平面内一点,且
所在平面内一点,且 ,则
,则 的最大值等于( ).
的最大值等于( ).
 ,
, ,
, ,若
,若 点是
点是 所在平面内一点,且
所在平面内一点,且 ,则
,则 的最大值等于( ).
的最大值等于( ).A. | B. | C. | D. |
10.若定义在 上的函数
上的函数 满足
满足 ,其导函数
,其导函数 满足
满足 ,则下列结论中一定错误的是( )
,则下列结论中一定错误的是( )
 上的函数
上的函数 满足
满足 ,其导函数
,其导函数 满足
满足 ,则下列结论中一定错误的是( )
,则下列结论中一定错误的是( )A. | B. |
C. | D. |
11. 的展开式中,
的展开式中,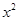 的系数等于 .(用数字作答)
的系数等于 .(用数字作答)
 的展开式中,
的展开式中,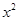 的系数等于 .(用数字作答)
的系数等于 .(用数字作答)12.若锐角 的面积为
的面积为 ,且
,且 ,则
,则 等于
等于_________ .
 的面积为
的面积为 ,且
,且 ,则
,则 等于
等于13.如图,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,函数
,函数 ,若在矩形
,若在矩形 内随机取一点,则此点取自阴影部分的概率等于
内随机取一点,则此点取自阴影部分的概率等于___________ .

 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,函数
,函数 ,若在矩形
,若在矩形 内随机取一点,则此点取自阴影部分的概率等于
内随机取一点,则此点取自阴影部分的概率等于
14.若函数 (
( 且
且 )的值域是
)的值域是 ,则实数
,则实数 的取值范围是
的取值范围是__________ .
 (
( 且
且 )的值域是
)的值域是 ,则实数
,则实数 的取值范围是
的取值范围是15.一个二元码是由0和1组成的数字串 ,其中
,其中 称为第
称为第 位码元,二元码是通信中常用的码,但在通信过程中有时会发生码元错误(即码元由0变为1,或者由1变为0)
位码元,二元码是通信中常用的码,但在通信过程中有时会发生码元错误(即码元由0变为1,或者由1变为0)
已知某种二元码 的码元满足如下校验方程组:
的码元满足如下校验方程组:
其中运算 定义为:
定义为: .
.
现已知一个这种二元码在通信过程中仅在第 位发生码元错误后变成了1101101,那么利用上述校验方程组可判定
位发生码元错误后变成了1101101,那么利用上述校验方程组可判定 等于 .
等于 .
 ,其中
,其中 称为第
称为第 位码元,二元码是通信中常用的码,但在通信过程中有时会发生码元错误(即码元由0变为1,或者由1变为0)
位码元,二元码是通信中常用的码,但在通信过程中有时会发生码元错误(即码元由0变为1,或者由1变为0)已知某种二元码
 的码元满足如下校验方程组:
的码元满足如下校验方程组:
其中运算
 定义为:
定义为: .
.现已知一个这种二元码在通信过程中仅在第
 位发生码元错误后变成了1101101,那么利用上述校验方程组可判定
位发生码元错误后变成了1101101,那么利用上述校验方程组可判定 等于 .
等于 .16.某银行规定,一张银行卡若在一天内出现3次密码尝试错误,该银行卡将被锁定,小王到银行取钱时,发现自己忘记了银行卡的密码,但是可以确定该银行卡的正确密码是他常用的6个密码之一,小王决定从中不重复地随机选择1个进行尝试.若密码正确,则结束尝试;否则继续尝试,直至该银行卡被锁定.
(Ⅰ)求当天小王的该银行卡被锁定的概率;
(Ⅱ)设当天小王用该银行卡尝试密码次数为X,求X的分布列和数学期望.
(Ⅰ)求当天小王的该银行卡被锁定的概率;
(Ⅱ)设当天小王用该银行卡尝试密码次数为X,求X的分布列和数学期望.
17.如图,在几何体ABCDE中,四边形ABCD是矩形,AB 平面BEC,BE
平面BEC,BE EC,AB=BE=EC=2,G,F分别是线段BE,DC的中点.
EC,AB=BE=EC=2,G,F分别是线段BE,DC的中点.

(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求平面AEF与平面BEC所成锐二面角的余弦值.
 平面BEC,BE
平面BEC,BE EC,AB=BE=EC=2,G,F分别是线段BE,DC的中点.
EC,AB=BE=EC=2,G,F分别是线段BE,DC的中点.
(Ⅰ)求证:
 平面
平面 ;
; (Ⅱ)求平面AEF与平面BEC所成锐二面角的余弦值.
18.已知椭圆 过点
过点 ,且离心率
,且离心率 .
.

(1)求椭圆 的方程;
的方程;
(2)设直 交椭圆
交椭圆 于
于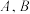 两点,判断点
两点,判断点 与以线段
与以线段 为直径的圆的位置关系,并说明理由.
为直径的圆的位置关系,并说明理由.
 过点
过点 ,且离心率
,且离心率 .
.
(1)求椭圆
 的方程;
的方程;(2)设直
 交椭圆
交椭圆 于
于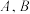 两点,判断点
两点,判断点 与以线段
与以线段 为直径的圆的位置关系,并说明理由.
为直径的圆的位置关系,并说明理由.19.已知函数 的图象是由函数
的图象是由函数 的图象经如下变换得到:先将
的图象经如下变换得到:先将 图象上所有点的纵坐标伸长到原来的
图象上所有点的纵坐标伸长到原来的 倍(横坐标不变),再将所得到的图象向右平移
倍(横坐标不变),再将所得到的图象向右平移 个单位长度.
个单位长度.
(1)求函数 的解析式,并求其图象的对称轴方程;
的解析式,并求其图象的对称轴方程;
(2) 已知关于 的方程
的方程 在
在 内有两个不同的解
内有两个不同的解 、
、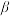 .
.
(i)求实数 的取值范围;
的取值范围;
(ii)证明: .
.
 的图象是由函数
的图象是由函数 的图象经如下变换得到:先将
的图象经如下变换得到:先将 图象上所有点的纵坐标伸长到原来的
图象上所有点的纵坐标伸长到原来的 倍(横坐标不变),再将所得到的图象向右平移
倍(横坐标不变),再将所得到的图象向右平移 个单位长度.
个单位长度.(1)求函数
 的解析式,并求其图象的对称轴方程;
的解析式,并求其图象的对称轴方程;(2) 已知关于
 的方程
的方程 在
在 内有两个不同的解
内有两个不同的解 、
、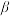 .
.(i)求实数
 的取值范围;
的取值范围;(ii)证明:
 .
.20.已知函数 ,
,
(Ⅰ)证明:当 ;
;
(Ⅱ)证明:当 时,存在
时,存在 ,使得对
,使得对

(Ⅲ)确定k的所以可能取值,使得存在 ,对任意的
,对任意的 恒有
恒有 .
.
 ,
,
(Ⅰ)证明:当
 ;
;(Ⅱ)证明:当
 时,存在
时,存在 ,使得对
,使得对

(Ⅲ)确定k的所以可能取值,使得存在
 ,对任意的
,对任意的 恒有
恒有 .
.21.本题设有三个选考题,请考生任选2题作答.
选修4-2:矩阵与变换
已知矩阵
(Ⅰ)求A的逆矩阵 ;
;
(Ⅱ)求矩阵C,使得AC=B.
选修4-2:矩阵与变换
已知矩阵

(Ⅰ)求A的逆矩阵
 ;
;(Ⅱ)求矩阵C,使得AC=B.
22.选修4-4:坐标系与参数方程
在平面直角坐标系 中,圆C的参数方程为
中,圆C的参数方程为 .在极坐标系(与平面直角坐标系
.在极坐标系(与平面直角坐标系 取相同的长度单位,且以原点O为极点,以
取相同的长度单位,且以原点O为极点,以 轴非负半轴为极轴)中,直线l的方程为
轴非负半轴为极轴)中,直线l的方程为
(Ⅰ)求圆C的普通方程及直线l的直角坐标方程;
(Ⅱ)设圆心C到直线l的距离等于2,求m的值.
在平面直角坐标系
 中,圆C的参数方程为
中,圆C的参数方程为 .在极坐标系(与平面直角坐标系
.在极坐标系(与平面直角坐标系 取相同的长度单位,且以原点O为极点,以
取相同的长度单位,且以原点O为极点,以 轴非负半轴为极轴)中,直线l的方程为
轴非负半轴为极轴)中,直线l的方程为
(Ⅰ)求圆C的普通方程及直线l的直角坐标方程;
(Ⅱ)设圆心C到直线l的距离等于2,求m的值.
23.已知 ,函数
,函数 的最小值为4.
的最小值为4.
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的最小值.
的最小值.
 ,函数
,函数 的最小值为4.
的最小值为4.(Ⅰ)求
 的值;
的值;(Ⅱ)求
 的最小值.
的最小值. 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
