搜索
全一卷
难度系数：0.65 
答案解析
有奖纠错
1．设
.则
________.
.则
________.2．化简
________.
________.3．已知等差数列
的前100项之和为100，最后100项之和为1000.则
________.
的前100项之和为100，最后100项之和为1000.则
________.4．记
表示不超过实数x的最大整数.则集合
共有________个元素.
表示不超过实数x的最大整数.则集合
共有________个元素.5．若关于x 的方程
有三个不同实根，则实数a的取值范围是________.
有三个不同实根，则实数a的取值范围是________.6．在单位正方体ABCD-A1B1C1D1中，O为正方形ABCD的中心，点M、N分别在棱A1D1、CC1上，
.则四面体OMNB1的体积 V = ________ .
.则四面体OMNB1的体积 V = 7．已知抛物线C以椭圆E的中心为焦点，抛物线C经过椭圆E的两个焦点，且与椭圆E恰有三个交点.则椭圆E的离心率为________.
8．等可能地随机产生一个正整数
.则x在二进制下的各位数字之和不超过8的概率为 ________.
.则x在二进制下的各位数字之和不超过8的概率为 ________.9．已知数列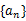
满足
，
用数学归纳法证明：
.
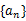满足
，
用数学归纳法证明：
.10．设
的内切圆与三边切于点D、E、
的内切圆与三边切于点D、E、A．证明：与 相似当且仅当为正三角形. |
11．证明：对任意实数a、b、c，均有
，并求等号成立的充分必要条件.
，并求等号成立的充分必要条件.12．求满足
的所有正整数数对（m，n）.
的所有正整数数对（m，n）.