全一卷
1.若 ,
, ,则
,则 的元素个数有( )。
的元素个数有( )。
 ,
, ,则
,则 的元素个数有( )。
的元素个数有( )。| A.4 | B.5 | C.8 | D.9 |
2.已知函数 且
且 ,则
,则 ( )
( )
 且
且 ,则
,则 ( )
( )| A.-5 | B.-3 | C.3 | D.随 的值而定 的值而定 |
3.集合 ,
, 的并集
的并集 ,当
,当 时,
时, 与
与 视为不同的对,则这样的
视为不同的对,则这样的 对的个数有( )。
对的个数有( )。
 ,
, 的并集
的并集 ,当
,当 时,
时, 与
与 视为不同的对,则这样的
视为不同的对,则这样的 对的个数有( )。
对的个数有( )。| A.8 | B.9 | C.26 | D.27 |
4.若直线 被曲线
被曲线 :
: 所截得的弦长为
所截得的弦长为 ,当
,当 变化时
变化时 的最小值是( ).
的最小值是( ).
 被曲线
被曲线 :
: 所截得的弦长为
所截得的弦长为 ,当
,当 变化时
变化时 的最小值是( ).
的最小值是( ).A. | B. | C. | D.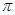 |
5.在 中,角
中,角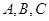 的对边边长分别是
的对边边长分别是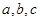 。若
。若 等于
等于 边上的高
边上的高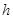 ,则
,则 的值是( )。
的值是( )。
 中,角
中,角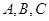 的对边边长分别是
的对边边长分别是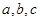 。若
。若 等于
等于 边上的高
边上的高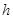 ,则
,则 的值是( )。
的值是( )。| A.1 | B.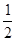 | C. | D.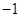 |
6.设 、
、 为非零实数,
为非零实数, 为虚数单位,
为虚数单位, .则方程
.则方程 与方程
与方程 在同一复平面内的图形(
在同一复平面内的图形( 、
、 为焦点)为( ).
为焦点)为( ).
 、
、 为非零实数,
为非零实数, 为虚数单位,
为虚数单位, .则方程
.则方程 与方程
与方程 在同一复平面内的图形(
在同一复平面内的图形( 、
、 为焦点)为( ).
为焦点)为( ).A. | B. | C. | D. |
7.二次方程 (
( 为虚数单位,
为虚数单位, )有两个虚根的充分必要条件是
)有两个虚根的充分必要条件是 的取值范围为______。
的取值范围为______。
 (
( 为虚数单位,
为虚数单位, )有两个虚根的充分必要条件是
)有两个虚根的充分必要条件是 的取值范围为______。
的取值范围为______。8.实数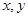 满足
满足 ,设
,设 ,则
,则 .
.
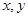 满足
满足 ,设
,设 ,则
,则 .
.9.若 ,
, ,
, ,则
,则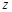 的值是______。
的值是______。
 ,
, ,
, ,则
,则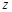 的值是______。
的值是______。10.整数 的末尾两位数字是______(先写十位数字,后写各位数字;其中
的末尾两位数字是______(先写十位数字,后写各位数字;其中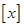 表示不超过
表示不超过 的最大整数)。
的最大整数)。
 的末尾两位数字是______(先写十位数字,后写各位数字;其中
的末尾两位数字是______(先写十位数字,后写各位数字;其中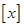 表示不超过
表示不超过 的最大整数)。
的最大整数)。11.设任意实数 。要使
。要使 恒成立,则
恒成立,则 的最大值是______。
的最大值是______。
 。要使
。要使 恒成立,则
恒成立,则 的最大值是______。
的最大值是______。12.三位数 共900个,在卡片上打印这些三位数,每张卡片打印一个三位数。有的卡片所印的,倒过来看仍为三位数,如198倒过来看是861(1倒过来看仍视为1);有的卡片则不然,如531倒过来看是
共900个,在卡片上打印这些三位数,每张卡片打印一个三位数。有的卡片所印的,倒过来看仍为三位数,如198倒过来看是861(1倒过来看仍视为1);有的卡片则不然,如531倒过来看是 。因此,有些卡片可以一卡二用,于是至多可少打印______张卡片。
。因此,有些卡片可以一卡二用,于是至多可少打印______张卡片。
 共900个,在卡片上打印这些三位数,每张卡片打印一个三位数。有的卡片所印的,倒过来看仍为三位数,如198倒过来看是861(1倒过来看仍视为1);有的卡片则不然,如531倒过来看是
共900个,在卡片上打印这些三位数,每张卡片打印一个三位数。有的卡片所印的,倒过来看仍为三位数,如198倒过来看是861(1倒过来看仍视为1);有的卡片则不然,如531倒过来看是 。因此,有些卡片可以一卡二用,于是至多可少打印______张卡片。
。因此,有些卡片可以一卡二用,于是至多可少打印______张卡片。13.三棱锥 中,侧棱
中,侧棱 两两互相垂直,
两两互相垂直, 为三角形
为三角形 的重心,
的重心, 为
为 中点,作与
中点,作与 平行的直线
平行的直线 .证明:
.证明:
(1) 写
写 相交;
相交;
(2)设 与
与 的交点为
的交点为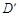 ,则
,则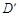 为三棱锥
为三棱锥 的外接球球心.
的外接球球心.
 中,侧棱
中,侧棱 两两互相垂直,
两两互相垂直, 为三角形
为三角形 的重心,
的重心, 为
为 中点,作与
中点,作与 平行的直线
平行的直线 .证明:
.证明:(1)
 写
写 相交;
相交;(2)设
 与
与 的交点为
的交点为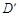 ,则
,则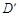 为三棱锥
为三棱锥 的外接球球心.
的外接球球心.14.设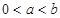 ,过两定点
,过两定点 和
和 分别引直线
分别引直线 和
和 ,使与抛物线
,使与抛物线 有四个不同的交点.当这四点共圆时,求这种直线
有四个不同的交点.当这四点共圆时,求这种直线 与
与 的交点
的交点 的轨迹.
的轨迹.
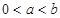 ,过两定点
,过两定点 和
和 分别引直线
分别引直线 和
和 ,使与抛物线
,使与抛物线 有四个不同的交点.当这四点共圆时,求这种直线
有四个不同的交点.当这四点共圆时,求这种直线 与
与 的交点
的交点 的轨迹.
的轨迹.15.设正数列 满足
满足
 ,且
,且 。求
。求 的通项公式。
的通项公式。
 满足
满足
 ,且
,且 。求
。求 的通项公式。
的通项公式。16.设一凸四边形 ,它的内角中仅有
,它的内角中仅有 是钝角.用一些直线段将该凸四边形分割成
是钝角.用一些直线段将该凸四边形分割成 个钝角三角形,但除去
个钝角三角形,但除去 外,在该凸四边形的周界上,不含分割出的钝角三角形顶点.试证
外,在该凸四边形的周界上,不含分割出的钝角三角形顶点.试证 应该满足的充分必要条件是
应该满足的充分必要条件是 .
.
 ,它的内角中仅有
,它的内角中仅有 是钝角.用一些直线段将该凸四边形分割成
是钝角.用一些直线段将该凸四边形分割成 个钝角三角形,但除去
个钝角三角形,但除去 外,在该凸四边形的周界上,不含分割出的钝角三角形顶点.试证
外,在该凸四边形的周界上,不含分割出的钝角三角形顶点.试证 应该满足的充分必要条件是
应该满足的充分必要条件是 .
.17.设 是一个有
是一个有 元素的集合,
元素的集合, 的
的 个子集
个子集 两两互不包含。试证:
两两互不包含。试证:
(1) ;
;
(2) 。
。
其中 表示
表示 所含元素的个数,
所含元素的个数, 表示
表示 个不同元素取
个不同元素取 个的组合数。
个的组合数。
 是一个有
是一个有 元素的集合,
元素的集合, 的
的 个子集
个子集 两两互不包含。试证:
两两互不包含。试证:(1)
 ;
;(2)
 。
。其中
 表示
表示 所含元素的个数,
所含元素的个数, 表示
表示 个不同元素取
个不同元素取 个的组合数。
个的组合数。18.水平直线 通过圆
通过圆 的中心,直线
的中心,直线 ,
, 与
与 相交于
相交于 ,点
,点 在圆心的右侧,直线
在圆心的右侧,直线 上不同的三点
上不同的三点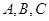 在圆外,且位于直线
在圆外,且位于直线 上方,
上方, 点离
点离 点最远,
点最远, 点离
点离 点最近,
点最近, 为圆
为圆 的三条切线,
的三条切线, 为切点。试证:
为切点。试证:
(1) 与圆
与圆 相切时,
相切时, ;
;
(2) 与圆
与圆 相交时,
相交时, ;
;
(3) 与圆
与圆 相离时,
相离时, 。
。
 通过圆
通过圆 的中心,直线
的中心,直线 ,
, 与
与 相交于
相交于 ,点
,点 在圆心的右侧,直线
在圆心的右侧,直线 上不同的三点
上不同的三点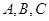 在圆外,且位于直线
在圆外,且位于直线 上方,
上方, 点离
点离 点最远,
点最远, 点离
点离 点最近,
点最近, 为圆
为圆 的三条切线,
的三条切线, 为切点。试证:
为切点。试证:(1)
 与圆
与圆 相切时,
相切时, ;
;(2)
 与圆
与圆 相交时,
相交时, ;
;(3)
 与圆
与圆 相离时,
相离时, 。
。 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
