全一卷
1.已知集合 则
则
_____ .
 则
则
2.复数 ,其中
,其中 为虚数单位,则
为虚数单位,则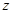 的实部为__________.
的实部为__________.
 ,其中
,其中 为虚数单位,则
为虚数单位,则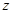 的实部为__________.
的实部为__________.3.在平面直角坐标系 中,双曲线
中,双曲线 的焦距是
的焦距是____________ .
 中,双曲线
中,双曲线 的焦距是
的焦距是4.已知一组数据4.7,4.8,5.1,5.4,5.5,则该组数据的方差是________.
5.函数y= 的定义域是 .
的定义域是 .
 的定义域是 .
的定义域是 .6.如图是一个算法的流程图,则输出的a的值是 .


7.将一颗质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,则出现向上的点数之和小于10的概率是 .
8.已知{ }是等差数列,
}是等差数列, 是其前
是其前 项和.若
项和.若 ,
, =10,则
=10,则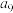 的值是
的值是_____ .
 }是等差数列,
}是等差数列, 是其前
是其前 项和.若
项和.若 ,
, =10,则
=10,则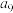 的值是
的值是9.定义在区间[0,3π]上的函数y=sin2x的图象与y=cosx的图象的交点个数是______ .
10.如图,在平面直角坐标系 中,F是椭圆
中,F是椭圆 的右焦点,直线
的右焦点,直线 与椭圆交于B,C两点,且
与椭圆交于B,C两点,且 ,则该椭圆的离心率是 .
,则该椭圆的离心率是 .

 中,F是椭圆
中,F是椭圆 的右焦点,直线
的右焦点,直线 与椭圆交于B,C两点,且
与椭圆交于B,C两点,且 ,则该椭圆的离心率是 .
,则该椭圆的离心率是 .
11.设 是定义在R上且周期为2的函数,在区间[
是定义在R上且周期为2的函数,在区间[ )上,
)上, 其中
其中 若
若 ,则
,则 的值是 .
的值是 .
 是定义在R上且周期为2的函数,在区间[
是定义在R上且周期为2的函数,在区间[ )上,
)上, 其中
其中 若
若 ,则
,则 的值是 .
的值是 .12.已知实数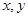 满足
满足 则
则 的取值范围是 .
的取值范围是 .
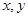 满足
满足 则
则 的取值范围是 .
的取值范围是 .13.如图,在 中,
中, 是
是 的中点,
的中点, 是
是 上的两个三等分点,
上的两个三等分点, ,
, ,则
,则 的值是
的值是_______ .

 中,
中, 是
是 的中点,
的中点, 是
是 上的两个三等分点,
上的两个三等分点, ,
, ,则
,则 的值是
的值是
14.在锐角三角形ABC中,若sinA=2sinBsinC,则tanAtanBtanC的最小值是 .
15.在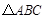 中,AC=6,
中,AC=6,
(1)求AB的长;
(2)求 的值.
的值.
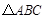 中,AC=6,
中,AC=6,
(1)求AB的长;
(2)求
 的值.
的值. 16.如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且 ,
, .
.

求证:(1)直线DE 平面A1C1F;
平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
 ,
, .
.
求证:(1)直线DE
 平面A1C1F;
平面A1C1F;(2)平面B1DE⊥平面A1C1F.
17.现需要设计一个仓库,它由上下两部分组成,上部分的形状是正四棱锥 ,下部分的形状是正四棱柱
,下部分的形状是正四棱柱 (如图所示),并要求正四棱柱的高
(如图所示),并要求正四棱柱的高 是正四棱锥的高
是正四棱锥的高 的4倍.
的4倍.

(1)若 则仓库的容积是多少?
则仓库的容积是多少?
(2)若正四棱锥的侧棱长为 ,则当
,则当 为多少时,仓库的容积最大?
为多少时,仓库的容积最大?
 ,下部分的形状是正四棱柱
,下部分的形状是正四棱柱 (如图所示),并要求正四棱柱的高
(如图所示),并要求正四棱柱的高 是正四棱锥的高
是正四棱锥的高 的4倍.
的4倍.
(1)若
 则仓库的容积是多少?
则仓库的容积是多少?(2)若正四棱锥的侧棱长为
 ,则当
,则当 为多少时,仓库的容积最大?
为多少时,仓库的容积最大?18.如图,在平面直角坐标系 中,已知以
中,已知以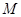 为圆心的圆
为圆心的圆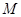 :
: 及其上一点A(2,4).
及其上一点A(2,4).

(1)设圆N与x轴相切,与圆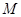 外切,且圆心N在直线x=6上,求圆N的标准方程;
外切,且圆心N在直线x=6上,求圆N的标准方程;
(2)设平行于OA的直线l与圆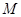 相交于B,C两点,且BC=OA,求直线l的方程;
相交于B,C两点,且BC=OA,求直线l的方程;
(3)设点T(t,0)满足:存在圆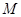 上的两点P和Q,使得
上的两点P和Q,使得 ,求实数t的取值范围.
,求实数t的取值范围.
 中,已知以
中,已知以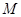 为圆心的圆
为圆心的圆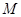 :
: 及其上一点A(2,4).
及其上一点A(2,4).
(1)设圆N与x轴相切,与圆
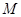 外切,且圆心N在直线x=6上,求圆N的标准方程;
外切,且圆心N在直线x=6上,求圆N的标准方程;(2)设平行于OA的直线l与圆
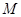 相交于B,C两点,且BC=OA,求直线l的方程;
相交于B,C两点,且BC=OA,求直线l的方程;(3)设点T(t,0)满足:存在圆
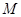 上的两点P和Q,使得
上的两点P和Q,使得 ,求实数t的取值范围.
,求实数t的取值范围.19.已知函数 .
.
(1)设 .
.
①求方程 =2的根;
=2的根;
②若对任意 ,不等式
,不等式 恒成立,求实数m的最大值;
恒成立,求实数m的最大值;
(2)若 ,函数
,函数 有且只有1个零点,求ab的值.
有且只有1个零点,求ab的值.
 .
.(1)设
 .
.①求方程
 =2的根;
=2的根;②若对任意
 ,不等式
,不等式 恒成立,求实数m的最大值;
恒成立,求实数m的最大值;(2)若
 ,函数
,函数 有且只有1个零点,求ab的值.
有且只有1个零点,求ab的值.20.记 .对数列
.对数列 和
和 的子集
的子集 ,若
,若 ,定义
,定义 ;若
;若 ,定义
,定义 .例如:
.例如: 时,
时, .现设
.现设 是公比为3的等比数列,且当
是公比为3的等比数列,且当 时,
时, .
.
(1)求数列 的通项公式;
的通项公式;
(2)对任意正整数 ,若
,若 ,求证:
,求证: ;
;
(3)设 ,求证:
,求证: .
.
 .对数列
.对数列 和
和 的子集
的子集 ,若
,若 ,定义
,定义 ;若
;若 ,定义
,定义 .例如:
.例如: 时,
时, .现设
.现设 是公比为3的等比数列,且当
是公比为3的等比数列,且当 时,
时, .
.(1)求数列
 的通项公式;
的通项公式;(2)对任意正整数
 ,若
,若 ,求证:
,求证: ;
;(3)设
 ,求证:
,求证: .
.21.[选修4-1几何证明选讲]如图,在 ABC中,∠ABC=90°,BD⊥AC,D为垂足,E是BC的中点.
ABC中,∠ABC=90°,BD⊥AC,D为垂足,E是BC的中点.

求证:∠EDC=∠ABD.
 ABC中,∠ABC=90°,BD⊥AC,D为垂足,E是BC的中点.
ABC中,∠ABC=90°,BD⊥AC,D为垂足,E是BC的中点.
求证:∠EDC=∠ABD.
22.[选修4-2:矩阵与变换]已知矩阵 矩阵B的逆矩阵
矩阵B的逆矩阵 ,求矩阵AB.
,求矩阵AB.
 矩阵B的逆矩阵
矩阵B的逆矩阵 ,求矩阵AB.
,求矩阵AB.23.[选修4-4:坐标系与参数方程]在平面直角坐标系xOy中,已知直线l的参数方程为 (t为参数),椭圆C的参数方程为
(t为参数),椭圆C的参数方程为 (
( 为参数).设直线l与椭圆C相交于A,B两点,求线段AB的长.
为参数).设直线l与椭圆C相交于A,B两点,求线段AB的长.
 (t为参数),椭圆C的参数方程为
(t为参数),椭圆C的参数方程为 (
( 为参数).设直线l与椭圆C相交于A,B两点,求线段AB的长.
为参数).设直线l与椭圆C相交于A,B两点,求线段AB的长.24.[选修4-5:不等式选讲]设a>0,|x 1|<
1|< ,|y
,|y 2|<
2|< ,求证:|2x+y
,求证:|2x+y 4|<a.
4|<a.
 1|<
1|< ,|y
,|y 2|<
2|< ,求证:|2x+y
,求证:|2x+y 4|<a.
4|<a.25.如图,在平面直角坐标系xOy中,已知直线l:x y
y 2=0,抛物线C:y2=2px(p>0).
2=0,抛物线C:y2=2px(p>0).

(1)若直线l过抛物线C的焦点,求抛物线C的方程;
(2)已知抛物线C上存在关于直线l对称的相异两点P和Q.
①求证:线段PQ的中点坐标为 ;
;
②求p的取值范围.
 y
y 2=0,抛物线C:y2=2px(p>0).
2=0,抛物线C:y2=2px(p>0).
(1)若直线l过抛物线C的焦点,求抛物线C的方程;
(2)已知抛物线C上存在关于直线l对称的相异两点P和Q.
①求证:线段PQ的中点坐标为
 ;
;②求p的取值范围.
26.(1)求 的值;
的值;
(2)设m,n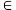 N*,n≥m,求证:
N*,n≥m,求证:
(m+1) +(m+2)
+(m+2) +(m+3)
+(m+3) +
+ +n
+n +(n+1)
+(n+1) =(m+1)
=(m+1) .
.
 的值;
的值;(2)设m,n
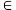 N*,n≥m,求证:
N*,n≥m,求证: (m+1)
 +(m+2)
+(m+2) +(m+3)
+(m+3) +
+ +n
+n +(n+1)
+(n+1) =(m+1)
=(m+1) .
. 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
