全一卷
1.已知集合 ,则
,则 ()
()
 ,则
,则 ()
()A. | B. | C. | D. |
2.“ ”是“
”是“ ”的
”的
 ”是“
”是“ ”的
”的| A.充要条件 | B.充分不必要条件 | C.必要不充分条件 | D.既不充分也不必要条件 |
3.函数 的定义域是
的定义域是
 的定义域是
的定义域是A. |
B. |
C. |
D. |
4.重庆市2013年各月的平均气温(°C)数据的茎叶图如下
则这组数据中的中位数是( )
| 0 | 8 | 9 | | | |
| 1 | 2 | 5 | 8 | | |
| 2 | 0 | 0 | 3 | 3 | 8 |
| 3 | 1 | 2 | | | |
则这组数据中的中位数是( )
| A.19 | B.20 | C.21.5 | D.23 |
5.某几何体的三视图如图所示,则该几何体的体积为( )


A. | B. | C. | D. |
6.若 ,则
,则
 ,则
,则
A. | B. | C. | D. |
7.已知非零向量 满足
满足 则
则 的夹角为()
的夹角为()
 满足
满足 则
则 的夹角为()
的夹角为()A. | B. | C. | D. |
8.执行如图所示的程序框图,则输出s的值为()


A. | B. | C. | D. |
9.设双曲线 的右焦点是F,左、右顶点分别是
的右焦点是F,左、右顶点分别是 ,过F做
,过F做 的垂线与双曲线交于B,C两点,若
的垂线与双曲线交于B,C两点,若 ,则双曲线的渐近线的斜率为
,则双曲线的渐近线的斜率为
 的右焦点是F,左、右顶点分别是
的右焦点是F,左、右顶点分别是 ,过F做
,过F做 的垂线与双曲线交于B,C两点,若
的垂线与双曲线交于B,C两点,若 ,则双曲线的渐近线的斜率为
,则双曲线的渐近线的斜率为A. | B. | C. | D. |
10.若不等式组 ,表示的平面区域为三角形,且其面积等于
,表示的平面区域为三角形,且其面积等于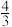 ,则m的值为
,则m的值为
 ,表示的平面区域为三角形,且其面积等于
,表示的平面区域为三角形,且其面积等于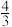 ,则m的值为
,则m的值为| A.-3 | B.1 | C.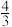 | D.3 |
11.复数 的实部为
的实部为________ .
 的实部为
的实部为12.若点 在以坐标原点为圆心的圆上,则该圆在点
在以坐标原点为圆心的圆上,则该圆在点 处的切线方程为
处的切线方程为__________ .
 在以坐标原点为圆心的圆上,则该圆在点
在以坐标原点为圆心的圆上,则该圆在点 处的切线方程为
处的切线方程为13.设 的内角
的内角 的对边分别为
的对边分别为 ,且
,且 ,则
,则
________ .
 的内角
的内角 的对边分别为
的对边分别为 ,且
,且 ,则
,则
14.设 ,则
,则 的最大值为
的最大值为 ________ .
 ,则
,则 的最大值为
的最大值为 15.在区间 上随机地选择一个数p,则方程
上随机地选择一个数p,则方程 有两个负根的概率为
有两个负根的概率为________ .
 上随机地选择一个数p,则方程
上随机地选择一个数p,则方程 有两个负根的概率为
有两个负根的概率为16.已知等差数列 满足
满足 ,前
,前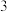 项和
项和 .
.
(1)求 的通项公式
的通项公式
(2)设等比数列 满足
满足 ,
, ,求
,求 的通项公式
的通项公式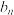 及
及 的前
的前 项和
项和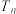 .
.
 满足
满足 ,前
,前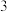 项和
项和 .
.(1)求
 的通项公式
的通项公式(2)设等比数列
 满足
满足 ,
, ,求
,求 的通项公式
的通项公式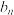 及
及 的前
的前 项和
项和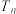 .
.17.随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:
(Ⅰ)求y关于t的回归方程
(Ⅱ)用所求回归方程预测该地区2015年( )的人民币储蓄存款.
)的人民币储蓄存款.
附:回归方程 中
中
| 年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
时间代号 | 1 | 2 | 3 | 4 | 5 |
储蓄存款 (千亿元) (千亿元) | 5 | 6 | 7 | 8 | 10 |
(Ⅰ)求y关于t的回归方程

(Ⅱ)用所求回归方程预测该地区2015年(
 )的人民币储蓄存款.
)的人民币储蓄存款.附:回归方程
 中
中
18.已知函数f(x)= sin2x-
sin2x-
 .
.
(Ⅰ)求f(x)的最小周期和最小值,
(Ⅱ)将函数f(x)的图象上每一点的横坐标伸长到原来的两倍,纵坐标不变,得到函数g(x)的图象.当x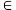
 时,求g(x)的值域.
时,求g(x)的值域.
 sin2x-
sin2x-
 .
.(Ⅰ)求f(x)的最小周期和最小值,
(Ⅱ)将函数f(x)的图象上每一点的横坐标伸长到原来的两倍,纵坐标不变,得到函数g(x)的图象.当x
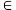
 时,求g(x)的值域.
时,求g(x)的值域.19.已知函数 在
在 处取得极值.
处取得极值.
 确定a的值;
确定a的值;
 若
若 ,讨论
,讨论 的单调性.
的单调性.
 在
在 处取得极值.
处取得极值. 确定a的值;
确定a的值; 若
若 ,讨论
,讨论 的单调性.
的单调性.20.如图,三棱锥P-ABC中,平面PAC 平面ABC,
平面ABC, ABC=
ABC= ,点D、E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF//BC.
,点D、E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF//BC.
(Ⅰ)证明:AB 平面PFE.
平面PFE.
(Ⅱ)若四棱锥P-DFBC的体积为7,求线段BC的长.

 平面ABC,
平面ABC, ABC=
ABC= ,点D、E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF//BC.
,点D、E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF//BC.(Ⅰ)证明:AB
 平面PFE.
平面PFE. (Ⅱ)若四棱锥P-DFBC的体积为7,求线段BC的长.

21.(本小题满分12分,(Ⅰ)小问5分,(Ⅱ)小问7分)
如图,椭圆 (
( >
> >0)的左右焦点分别为
>0)的左右焦点分别为 ,
, ,且过
,且过 的直线交椭圆于P,Q两点,且PQ
的直线交椭圆于P,Q两点,且PQ
 .
.

(Ⅰ)若| |=2+
|=2+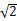 ,|
,| |=2-
|=2-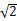 ,求椭圆的标准方程.
,求椭圆的标准方程.
(Ⅱ)若|PQ|= |
| |,且
|,且
 ,试确定椭圆离心率的取值范围.
,试确定椭圆离心率的取值范围.
如图,椭圆
 (
( >
> >0)的左右焦点分别为
>0)的左右焦点分别为 ,
, ,且过
,且过 的直线交椭圆于P,Q两点,且PQ
的直线交椭圆于P,Q两点,且PQ
 .
.
(Ⅰ)若|
 |=2+
|=2+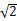 ,|
,| |=2-
|=2-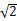 ,求椭圆的标准方程.
,求椭圆的标准方程.(Ⅱ)若|PQ|=
 |
| |,且
|,且
 ,试确定椭圆离心率的取值范围.
,试确定椭圆离心率的取值范围. 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
